【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

参考答案:
【答案】(1) △ABC面积是![]() ;(2)
;(2)![]() ;(3)S△ABC =
;(3)S△ABC =![]()
【解析】分析:(1)直接代入海伦公式计算.(2)利用海伦公式求出面积,再用一般求三角形面积公式求高.(2)角平分线的交点,到各个边的距离相等,所以可以用三个三角形的面积等于总面积,且高都相等,列方程可求出角分线到各边的距离.
详解:
(1)![]() =12
=12![]() △ABC面积是
△ABC面积是![]() .
.
(2)等面积法求出![]() ,
, ![]()
![]()
(3)如图,过点I作IF⊥AB、IG⊥AC、IH⊥BC,垂足分别为点F、G、H,
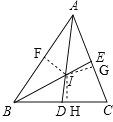
∵AD、BE分别为△ABC的角平分线,∴IF=IH=IG,
∵S△ABC=S△ABI+S△ACI+S△BCI, ∴![]() (9IF+8IF+7IF)=
(9IF+8IF+7IF)=![]() ,解得IF=
,解得IF=![]()
故S△ABC =![]() ABFI=
ABFI=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB'C',若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )

A.
π
B.
π
C.2π
D.4π -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3
 ﹣(+2
﹣(+2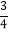 )﹣(﹣2
)﹣(﹣2 )﹣(﹣0.75);
)﹣(﹣0.75);(2)(
 ﹣
﹣ +
+ )×(﹣78);
)×(﹣78);(3)(﹣
 )÷(1
)÷(1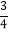 ﹣
﹣ ﹣
﹣ );
);(4)﹣32﹣2÷
 ×[2﹣(﹣
×[2﹣(﹣ )2]﹣(﹣2)3.
)2]﹣(﹣2)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两条边长分别是7和3,第三边长为整数,则这个三角形的周长是偶数的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,一次函数y=kx+b的图象与反比例函数
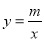 的图象交于
的图象交于 ,
,  两点.
两点.(1)求一次函数和反比例函数的解析式;
(2)设点
 和
和 是反比例函数
是反比例函数 图象上两点,若
图象上两点,若 ,求
,求 的值;
的值;(3)若M(x1,y1)和N(x2,y2)两点在直线AB上,如图2所示,过M、N两点分别作y轴的平行线交双曲线于E、F,已知﹣3<x1<0,x2>1,请探究当x1、x2满足什么关系时,MN∥EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学的学习过程中,我们要善于观察、发现规律并总结、应用.下面给同学们展示了四种有理数的简便运算的方法:
方法①:(﹣
 )2×162=[(﹣
)2×162=[(﹣ )×16]2=(﹣8)2=64,23×53=(2×5)3=103=1000
)×16]2=(﹣8)2=64,23×53=(2×5)3=103=1000规律:a2b2=(ab)2,anbn=(ab)n (n为正整数)
方法②:3.14×23+3.14×17+3.14×60=3.14×(23+17+60)=3.14×100=314
规律:ma+mb+mc=m(a+b+c)
方法③:(﹣12
 )÷3=[(﹣12)+(﹣
)÷3=[(﹣12)+(﹣ )]×
)]× =(﹣12)×
=(﹣12)× +(﹣
+(﹣ )×
)× =(﹣4)+(﹣
=(﹣4)+(﹣ )=﹣4
)=﹣4
方法④:
 =1﹣
=1﹣ ,
, =
= ﹣
﹣ ,
, =
= ﹣
﹣ ,
, =
= ﹣
﹣ ,…
,…规律:
 =
= ﹣
﹣ (n为正整数)
(n为正整数)利用以上方法,进行简便运算:
①(﹣0.125)2014×82014;
②  ×(﹣
×(﹣ )﹣(﹣
)﹣(﹣ )×(﹣
)×(﹣ )﹣
)﹣ ×2
×2 ;
;③(﹣20
 )÷(﹣5);
)÷(﹣5); ④
 +
+ +
+ +…+
+…+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.

相关试题

