【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB'C',若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
A.![]()
π
B.![]()
π
C.2π
D.4π
参考答案:
【答案】C
【解析】解:扇形BAB′的面积是: ![]() =
= ![]() , 在直角△ABC中,BC=ABsin60°=4×
, 在直角△ABC中,BC=ABsin60°=4× ![]() =2
=2 ![]() ,AC=
,AC= ![]() AB=2,S△ABC=S△AB′C′=
AB=2,S△ABC=S△AB′C′= ![]() ACBC=
ACBC= ![]() ×2
×2 ![]() ×2=2
×2=2 ![]() .扇形CAC′的面积是:
.扇形CAC′的面积是: ![]() =
= ![]() ,则阴影部分的面积是:扇形BAB′的面积+S△AB′C′﹣S△ABC﹣扇形CAC′的面积=
,则阴影部分的面积是:扇形BAB′的面积+S△AB′C′﹣S△ABC﹣扇形CAC′的面积= ![]() ﹣
﹣ ![]() =2π.
=2π.
故选:C.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2),以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为 ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数 的图象经过C点.
的图象经过C点.(1)求该反比例函数的解析式;
(2)当函数值
 >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
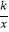 (k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( )
(k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( )
A.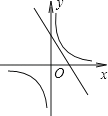
B.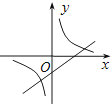
C.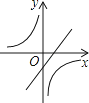
D.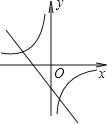
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知分式A=
 .
.(1) 化简这个分式;
(2) 当a>2时,把分式A化简结果的分子与分母同时加上3后得到分式B,问:分式B的值较原来分式A的值是变大了还是变小了?试说明理由.
(3) 若A的值是整数,且a也为整数,求出符合条件的所有a值的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3
 ﹣(+2
﹣(+2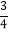 )﹣(﹣2
)﹣(﹣2 )﹣(﹣0.75);
)﹣(﹣0.75);(2)(
 ﹣
﹣ +
+ )×(﹣78);
)×(﹣78);(3)(﹣
 )÷(1
)÷(1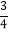 ﹣
﹣ ﹣
﹣ );
);(4)﹣32﹣2÷
 ×[2﹣(﹣
×[2﹣(﹣ )2]﹣(﹣2)3.
)2]﹣(﹣2)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两条边长分别是7和3,第三边长为整数,则这个三角形的周长是偶数的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为
 ,其中
,其中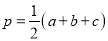 .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为
 ,AC边上的高
,AC边上的高 ,求
,求 的值;
的值;(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

相关试题

