搜索
【题目】已知三角形的两条边长分别是7和3，第三边长为整数，则这个三角形的周长是偶数的概率是 ．
参考答案：
【答案】
【解析】解：设第三边长为xcm．
则有7﹣3＜x＜7+3，
即4＜x＜10，
当第三边长为整数时，x=5或6或7或8或9，
当这个三角形的周长是偶数时，
x=6或8，
则这个三角形的周长是偶数的概率是 ．所以答案是： ．
【考点精析】关于本题考查的一元一次不等式组的整数解和三角形三边关系，需要了解使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)；三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知分式A=
.(1) 化简这个分式；
(2) 当a＞2时，把分式A化简结果的分子与分母同时加上3后得到分式B，问：分式B的值较原来分式A的值是变大了还是变小了？试说明理由.
(3) 若A的值是整数，且a也为整数，求出符合条件的所有a值的和.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°．把△ABC绕点A按顺时针方向旋转60°后得到△AB'C'，若AB=4，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是（ ）
A.
π
B.
π
C.2π
D.4π -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）3
﹣（+2
）﹣（﹣2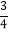
）﹣（﹣0.75）；（2）（
﹣
+
）×（﹣78）；（3）（﹣
）÷（1﹣﹣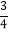
）；（4）﹣32﹣2÷
×[2﹣（﹣
）2]﹣（﹣2）3． -
科目： 来源： 题型：
查看答案和解析>>【题目】数学阅读：
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式：若一个三角形的三边长分别为a、b、c，则这个三角形的面积为
，其中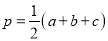
.这个公式称为“海伦公式”．数学应用：
如图1，在△ABC中，已知AB=9，AC=8，BC=7.
（1）请运用海伦公式求△ABC的面积；
（2）设AB边上的高为
，AC边上的高
，求
的值；（3）如图2，AD、BE为△ABC的两条角平分线，它们的交点为I，求△ABI的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1所示，一次函数y=kx+b的图象与反比例函数
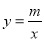的图象交于
， 
两点．（1）求一次函数和反比例函数的解析式；
（2）设点
和
是反比例函数
图象上两点,若
，求
的值；（3）若M（x1，y1）和N（x2，y2）两点在直线AB上，如图2所示，过M、N两点分别作y轴的平行线交双曲线于E、F，已知﹣3＜x1＜0，x2＞1，请探究当x1、x2满足什么关系时，MN∥EF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数学的学习过程中，我们要善于观察、发现规律并总结、应用．下面给同学们展示了四种有理数的简便运算的方法：
方法①：（﹣
）2×162=[（﹣）×16]2=（﹣8）2=64，23×53=（2×5）3=103=1000规律：a2b2=（ab）2，anbn=（ab）n （n为正整数）
方法②：3.14×23+3.14×17+3.14×60=3.14×（23+17+60）=3.14×100=314
规律：ma+mb+mc=m（a+b+c）
方法③：（﹣12
）÷3=[（﹣12）+（﹣）]×
=（﹣12）×+（﹣）×=（﹣4）+（﹣
）=﹣4方法④：
=1﹣，
=﹣，
=﹣，
=﹣
，…规律：
=
﹣
（n为正整数）利用以上方法，进行简便运算：
①（﹣0.125）2014×82014；
② 
×（﹣
）﹣（﹣
）×（﹣）﹣×2
；③（﹣20
）÷（﹣5）； ④
+++…+
．
相关试题
