【题目】在数学的学习过程中,我们要善于观察、发现规律并总结、应用.下面给同学们展示了四种有理数的简便运算的方法:
方法①:(﹣![]() )2×162=[(﹣
)2×162=[(﹣![]() )×16]2=(﹣8)2=64,23×53=(2×5)3=103=1000
)×16]2=(﹣8)2=64,23×53=(2×5)3=103=1000
规律:a2b2=(ab)2,anbn=(ab)n (n为正整数)
方法②:3.14×23+3.14×17+3.14×60=3.14×(23+17+60)=3.14×100=314
规律:ma+mb+mc=m(a+b+c)
方法③:(﹣12![]() )÷3=[(﹣12)+(﹣
)÷3=[(﹣12)+(﹣![]() )]×
)]×![]() =(﹣12)×
=(﹣12)×![]() +(﹣
+(﹣![]() )×
)×![]() =(﹣4)+(﹣
=(﹣4)+(﹣![]() )=﹣4
)=﹣4![]()
方法④:![]() =1﹣
=1﹣![]() ,
,![]() =
=![]() ﹣
﹣![]() ,
,![]() =
=![]() ﹣
﹣![]() ,
,![]() =
=![]() ﹣
﹣![]() ,…
,…
规律:![]() =
=![]() ﹣
﹣![]() (n为正整数)
(n为正整数)
利用以上方法,进行简便运算:
①(﹣0.125)2014×82014;
![]() ×(﹣
×(﹣![]() )﹣(﹣
)﹣(﹣![]() )×(﹣
)×(﹣![]() )﹣
)﹣![]() ×2
×2![]() ;
;
③(﹣20![]() )÷(﹣5);
)÷(﹣5);
④![]() +
+![]() +
+![]() +…+
+…+![]() .
.
参考答案:
【答案】(1)1 (2)-![]() (3)
(3)![]() (4)
(4)![]()
【解析】
(1)、首先将底数进行相乘,然后进行幂的计算;(2)、利用乘法分配律的逆运算进行求值即可得出答案;(3)、首先将除法改成乘法,然后再利用乘法分配律进行计算;(4)、根据给出的例题进行裂项相消,从而得出答案.
①原式=[(﹣0.125)×8]2014=(﹣1)2014=1;
②原式=(﹣![]() )×(
)×(![]() +
+![]() +2
+2![]() )=(﹣
)=(﹣![]() )×
)×![]() =﹣
=﹣![]() ;
;
③原式=[(﹣20)+(﹣![]() )]×(﹣
)]×(﹣![]() )=(﹣20)×(﹣
)=(﹣20)×(﹣![]() )+(﹣
)+(﹣![]() )×(﹣
)×(﹣![]() )
)
=4+![]() =
=![]() ;
;
④原式=(1﹣![]() )+(
)+(![]() ﹣
﹣![]() )+(
)+(![]() ﹣
﹣![]() )+…+
)+…+![]() ﹣
﹣![]()
=1﹣![]() +
+![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]() =1﹣
=1﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两条边长分别是7和3,第三边长为整数,则这个三角形的周长是偶数的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为
 ,其中
,其中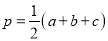 .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为
 ,AC边上的高
,AC边上的高 ,求
,求 的值;
的值;(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,一次函数y=kx+b的图象与反比例函数
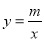 的图象交于
的图象交于 ,
,  两点.
两点.(1)求一次函数和反比例函数的解析式;
(2)设点
 和
和 是反比例函数
是反比例函数 图象上两点,若
图象上两点,若 ,求
,求 的值;
的值;(3)若M(x1,y1)和N(x2,y2)两点在直线AB上,如图2所示,过M、N两点分别作y轴的平行线交双曲线于E、F,已知﹣3<x1<0,x2>1,请探究当x1、x2满足什么关系时,MN∥EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,则线段EF的长是cm.

-
科目: 来源: 题型:
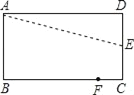
查看答案和解析>>【题目】如图,折叠形ABCD的一边AD,点D落在BC边上的点F处,AE是折痕,已知AB=8cm,BC=10cm.则CE=__cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC的两边分别平行于∠DEF的两条边,且∠ABC=45°.
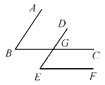
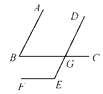
图1 图2
(1)图1中:∠DEF=_________,图2中:∠DEF=_________;
(2)请观察图1、图2中∠DEF分别与∠ABC有怎样的关系,请你归纳出一个命题.
相关试题

