【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
.
(1)在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿 ![]() 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
参考答案:
【答案】
(1)
如图, 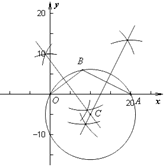
⊙C即为所求作的圆
(2)
B(8,6)
cos ![]() =
= ![]()
(3)
点B沿 ![]() 轴向右平移2个单位或
轴向右平移2个单位或 ![]() 或
或 ![]() 个单位
个单位
【解析】(1)如图,分别作OB,OA的垂直平分线,得到它们的交点,再画圆,详细方法:
画OB的垂直平分线:分别以O,B为圆心,以大于![]() OB的长度画弧,在OB的两侧相交于两点,连接它们,即是OB的垂直平分线;
OB的长度画弧,在OB的两侧相交于两点,连接它们,即是OB的垂直平分线;
画AB的垂直平分线:分别以A,B为圆心,以大于![]() AB的长度画弧,在OB的两侧相交于两点,连接它们,即是AB的垂直平分线;
AB的长度画弧,在OB的两侧相交于两点,连接它们,即是AB的垂直平分线;
得到交点C,即是外接圆的圆心,以OC为半径画圆.![]()
![]()

 (2)如图1,过点B作BD
(2)如图1,过点B作BD![]() OA于D,则在Rt
OA于D,则在Rt![]() OBD中,sin∠BOA=
OBD中,sin∠BOA= ![]() , BO=10,
, BO=10,
则BD=OB×sin∠BOA=10×![]() =6,
=6,
则OD=![]() .
.
则B(8,6).
在Rt![]() ABD中,因为A(20,0),则OA=20,AD=OA-OD=20-8=12,AB=
ABD中,因为A(20,0),则OA=20,AD=OA-OD=20-8=12,AB=![]() ,
,
则cos ∠ BAO=![]() .
.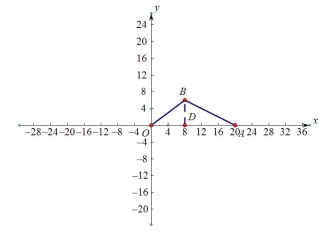
图1
(3)以OA为底时,如图2,OB=AB,则B(10,6),向x轴正方向平移了10-8=2;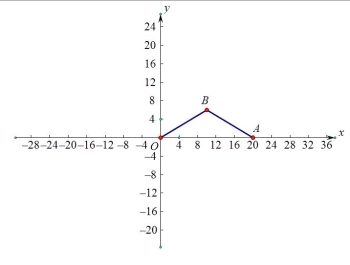
图2
以OB为底边时,如图3,AB=OA=20,则AD=![]() ,
,
则OD=OA-AD或OA+AD,即OD=![]() 或
或![]() ,
,
所以向x轴正半轴移动了18![]() <0,不符合,合去,或
<0,不符合,合去,或![]() ;
;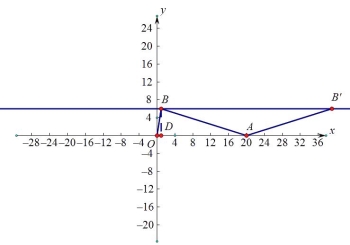
图3
以AB为底时,如图4,OB=OA=20,则OD=![]() ,
,
所以向x轴正半轴移动了![]() .
.
综上,答案为:点B沿 ![]() 轴向右平移2个单位或
轴向右平移2个单位或![]() 或
或![]() 个单位
个单位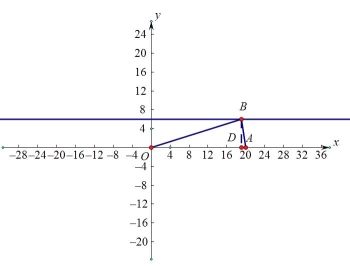
图4
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对三角形的外接圆与外心的理解,了解过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某长方形广场的四角都有一块半径相同的
 圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.
圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.(1)请列式表示广场空地的面积;

(2)若长方形的长为300米,宽为200米,圆形的半径为10米,计算广场空地的面积(计算结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,AB与y轴的交点坐标D为(0,4)。求A、B的坐标.
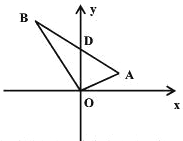
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6
 ,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标. 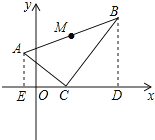
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
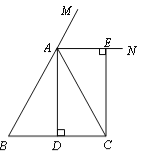
-
科目: 来源: 题型:
查看答案和解析>>【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.
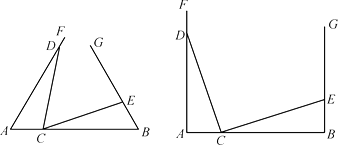
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
相关试题

