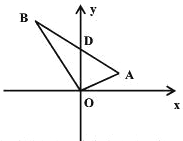
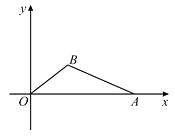
【题目】如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,AB与y轴的交点坐标D为(0,4)。求A、B的坐标.
参考答案:
【答案】点A的坐标为(2![]() ,2);点B的坐标为:(-2
,2);点B的坐标为:(-2![]() ,6).
,6).
【解析】分析:首先过点A作AC⊥x轴于点C,由直角三角形OAB中,∠AOB=90°,∠A=60°,∠BOD=30°,易得△AOD是等边三角形,即可求得OA的长,然后由含30°角的直角三角形的性质,求得AC的长,由勾股定理即可求得OC的长,则可求得答案.
详解:
过点A作AC⊥x轴于点C,

∵直角三角形OAB中,∠AOB=90°,∠A=60°,∠BOD=30°,
∴∠AOD=∠AOB-∠BOD=60°,
∴∠AOD=∠A,
∴OA=OD,
∴△AOD是等边三角形,
∵点D的坐标为(0,4),
∴OA=OD=4,
∵∠AOC=90°-∠AOD=30°,
∴AC=![]() OA=2,
OA=2,
∴OC=![]() ,
,
∴点A的坐标为:(2![]() ,2).
,2).
同理可得,点B的坐标为:(-2![]() ,6).
,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,CD、C′D′分别是Rt△ABC,Rt△A′B′C′斜边上的高,且CB=C′B′,CD=C′D′.求证:△ABC≌△A′B′C′.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某长方形广场的四角都有一块半径相同的
 圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.
圆形的草地,已知圆形的半径为r米,长方形的长为a米,宽为b米.(1)请列式表示广场空地的面积;

(2)若长方形的长为300米,宽为200米,圆形的半径为10米,计算广场空地的面积(计算结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6
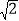 ,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标. 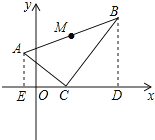
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
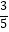 .
.
(1)在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹)
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离. -
科目: 来源: 题型:
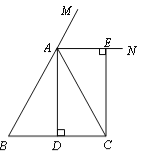
查看答案和解析>>【题目】(10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
相关试题

