【题目】在数轴上点A表示整数a,且![]() ,点B表示a的相反数.
,点B表示a的相反数.
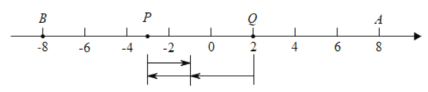
(1)画数轴,并在数轴上标出点A与点B;
(2)点P, Q 在线段AB上,且点P在点Q的左侧,若P, Q两点沿数轴相向匀速运动,出发后经4秒两点相遇. 已知在相遇时点Q比点P多行驶了3个单位,相遇后经1秒点Q到达点P的起始位置. 问点P、Q运动的速度分别是每秒多少个单位;.
(3)在(2)的条件下,若点P从整数点出发,当运动时间为t秒时(t是整数),将数轴折叠,使A点与B点重合,经过折叠P点与Q点也恰好重合,求P点的起始位置表示的数.
参考答案:
【答案】(1)![]() ; (2)点P是
; (2)点P是![]() 个单位/秒;点Q是1个单位/秒;(3)P点的起始位置表示的数为-1或2.
个单位/秒;点Q是1个单位/秒;(3)P点的起始位置表示的数为-1或2.
【解析】
(1)![]() ,找55到65之间的完全平方数可求得
,找55到65之间的完全平方数可求得![]() ,b=-8,在数轴上表示即可;
,b=-8,在数轴上表示即可;
(2)出发4秒后在相遇时点Q比点P多行驶了3个单位,可得关系式![]() .分析可得Q的速度是P的速度的4倍,设P的速度为x单位/秒,则Q的速度为4x单位/秒,可得
.分析可得Q的速度是P的速度的4倍,设P的速度为x单位/秒,则Q的速度为4x单位/秒,可得![]() ,于是可解;
,于是可解;
(3)由(2)可知:P的速度为和Q的速度,于是可求PQ的长. 折点为AB中点是原点,P,Q表示的数互为相反数,据此可解.
解:(1)![]() ,找55到65之间的完全平方数
,找55到65之间的完全平方数
![]() ,所以
,所以![]() ,b=-8
,b=-8

(2)
∵出发4秒后在相遇时点Q比点P多行驶了3个单位
∴可得关系式![]()
∵P从初始点到相遇点经过的时间为4s
Q从相遇点到P的初始点经过的时间为1s
∴可得Q的速度是P的速度的4倍
∴设P的速度为x单位/秒,则Q的速度为4x单位/秒
∴![]() ,
,![]()
代入关系式得
![]()
解得 ![]()
则Q的速度为![]() 单位/秒
单位/秒
答:P的速度为![]() 单位/秒,Q的速度为1单位/秒
单位/秒,Q的速度为1单位/秒
(3)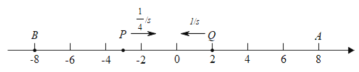
由(2)可知:P的速度为![]() 单位/秒,Q的速度为1单位/秒
单位/秒,Q的速度为1单位/秒
PQ=![]()
由题意,折叠后A,B重合,因此折点为AB中点,即![]()
又∵P,Q运动t秒后,折叠重合,且折点为原点
∴P,Q表示的数互为相反数
设P从y点出发,则Q从(y+5)出发
则P:![]() Q:
Q:![]()
∵P,Q互为相反数
![]()
![]()
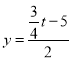
![]()
∵y,t均为整数
且![]()
∴解得![]() 或
或![]()
综上所述:P从-1或2出发满足条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, ,
, ,点
,点 是
是 边上的中点,点
边上的中点,点 是
是 上的一动点(不与点
上的一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连结
,连结 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形;
是平行四边形; 填空:①当
填空:①当 ________时,四边形
________时,四边形 是矩形;②当
是矩形;②当 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
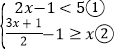
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)α= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
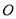 为直线
为直线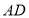 上一点,
上一点,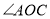 与
与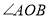 互补,
互补,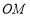 、
、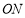 分别是
分别是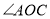 、
、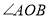 的平分线,
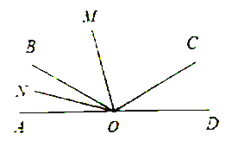
的平分线,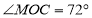 .
.
(1)
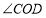 与
与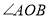 相等吗?请说明理由;
相等吗?请说明理由;(2)求
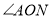 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节放假期间,某学校计划租用
 辆客车送
辆客车送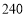 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车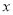 辆,租车总费用为
辆,租车总费用为 元.
元.甲种客车
乙种客车
载客量(人/辆)
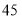
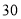
租金(元/辆)
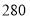
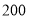
(1)求出
 (元)与
(元)与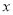 (辆)之间函数关系式;
(辆)之间函数关系式;(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为
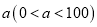 千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.(1)设客车行驶时间为
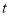 (小时),当
(小时),当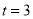 时,客车与乙城的距离为_______千米(用含
时,客车与乙城的距离为_______千米(用含 的代数式表示);
的代数式表示);(2)已知
 ,丙城在甲、乙两城之间,且与甲城相距260千米.
,丙城在甲、乙两城之间,且与甲城相距260千米.①求客车与出租车相距200千米时客车的行驶时间;(列方程解答)
②已知客车和出租车在甲、乙之间的
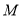 处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油的时间忽略不计;
方案二:在
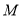 处换乘客车返回乙城.
处换乘客车返回乙城.试通过计算,分析小李选择哪种方案能更快到达乙城?
相关试题

