【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
(1)设客车行驶时间为![]() (小时),当
(小时),当![]() 时,客车与乙城的距离为_______千米(用含
时,客车与乙城的距离为_______千米(用含![]() 的代数式表示);
的代数式表示);
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米.
,丙城在甲、乙两城之间,且与甲城相距260千米.
①求客车与出租车相距200千米时客车的行驶时间;(列方程解答)
②已知客车和出租车在甲、乙之间的![]() 处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油的时间忽略不计;
方案二:在![]() 处换乘客车返回乙城.
处换乘客车返回乙城.
试通过计算,分析小李选择哪种方案能更快到达乙城?
参考答案:
【答案】(1)(800-3a);(2)小李选择方案一能更快到达乙城.
【解析】
(1)根据剩下的路程=总路程-已行驶的路程即可得到答案;
(2)①设当客车与出租车相距200千米时客车的行驶时间是![]() 小时,分相遇前、相遇后两种情况列方程解答;
小时,分相遇前、相遇后两种情况列方程解答;
②设客车和出租车x小时相遇,列方程求出x的值得到丙城与M处之间的距离为60km,再分别计算两种方案所需的时间即可得到答案.
(1)客车已行驶的路程是3a千米,
∴当![]() 时,客车与乙城的距离为(800-3a),
时,客车与乙城的距离为(800-3a),
故答案为:(800-3a);
(2)①设当客车与出租车相距200千米时客车的行驶时间是![]() 小时,
小时,
a:当客车和出租车没有相遇时,
60![]() +90
+90![]() +200=800 ,
+200=800 ,
解得![]() =4,
=4,
b:当客车和出租车相遇后,
60![]() +90
+90![]() -200=800,
-200=800,
解得:![]() =
=![]() ,
,
当客车与出租车相距200千米时客车的行驶时间是4小时或![]() 小时;
小时;
②设客车和出租车x小时相遇,
60x+90x=800 ,
∴x=![]() ,
,
此时客车走的路程为320km,出租车走的路程为480km,
∴丙城与M处之间的距离为60km,
方案一:小李需要的时间是(60+60+480)![]() 90=
90=![]() =
=![]() 小时;
小时;
方案二:小李需要的时间是480![]() 60=8小时.
60=8小时.
∵![]() <8,
<8,
∴小李选择方案一能更快到达乙城.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示整数a,且
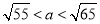 ,点B表示a的相反数.
,点B表示a的相反数.(1)画数轴,并在数轴上标出点A与点B;
(2)点P, Q 在线段AB上,且点P在点Q的左侧,若P, Q两点沿数轴相向匀速运动,出发后经4秒两点相遇. 已知在相遇时点Q比点P多行驶了3个单位,相遇后经1秒点Q到达点P的起始位置. 问点P、Q运动的速度分别是每秒多少个单位;.
(3)在(2)的条件下,若点P从整数点出发,当运动时间为t秒时(t是整数),将数轴折叠,使A点与B点重合,经过折叠P点与Q点也恰好重合,求P点的起始位置表示的数.
-
科目: 来源: 题型:
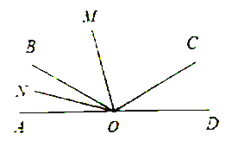
查看答案和解析>>【题目】如图,已知
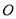 为直线
为直线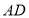 上一点,
上一点,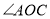 与
与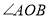 互补,
互补,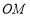 、
、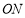 分别是
分别是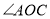 、
、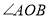 的平分线,
的平分线,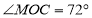 .
.
(1)
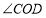 与
与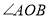 相等吗?请说明理由;
相等吗?请说明理由;(2)求
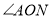 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节放假期间,某学校计划租用
 辆客车送
辆客车送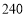 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车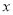 辆,租车总费用为
辆,租车总费用为 元.
元.甲种客车
乙种客车
载客量(人/辆)
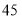
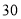
租金(元/辆)
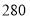
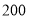
(1)求出
 (元)与
(元)与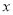 (辆)之间函数关系式;
(辆)之间函数关系式;(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学学生在学习等腰三角形性质“三线合一”时
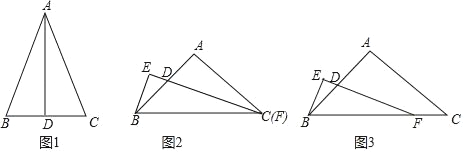
(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D为BC中点,请用所学知识证明此结论.
(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=
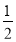 ∠ACB,试探究线段BE和FD的数量关系,并证明.
∠ACB,试探究线段BE和FD的数量关系,并证明.(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=
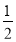 ∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论. -
科目: 来源: 题型:
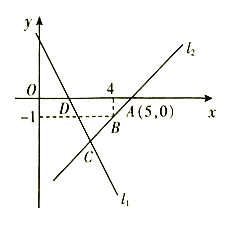
查看答案和解析>>【题目】如图,直线
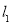 的函数解析式为
的函数解析式为 ,且
,且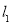 与
与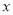 轴交于点
轴交于点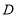 ,直线
,直线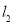 经过点
经过点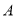 、
、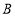 ,直线
,直线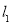 、
、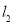 交于点
交于点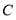 .
.
(1)求直线
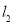 的函数解析式;
的函数解析式;(2)求
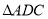 的面积;
的面积;(3)在直线
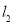 上是否存在点
上是否存在点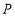 ,使得
,使得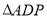 面积是
面积是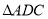 面积的
面积的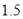 倍?如果存在,请求出
倍?如果存在,请求出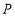 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,D为⊙O上一点,过
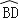 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=
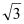 ,求AD的长.
,求AD的长.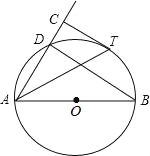
相关试题

