搜索
【题目】计算：﹣33= ．
参考答案：
【答案】-27
【解析】解：原式=﹣33=﹣27．所以答案是：﹣27．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系xoy中，已知点P是反比例函数
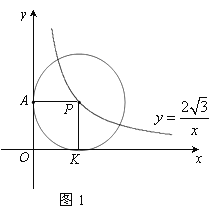
图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：
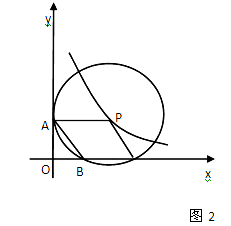
①求出点A，B，C的坐标．
②在P点右侧的反比例函数
图像是否存在上点M，使△MBP的面积等于菱形ABCP面积．若存在，试求出满足条件的M点的坐标，若不存在，试说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F.将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N, 有下列四个结论：① DF=CF；② BF⊥EN；③△BEN是等边三角形；④ S△BEF=3S△DEF. 其中，正确的结论有（ ）
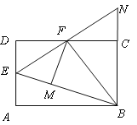
A．1个 B．2个 C．3个 D．4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y＝2x2，y＝－2x2，y＝2x2＋1共有的性质是
A. 开口向上 B. 对称轴都是y轴 C. 都有最高点 D. 顶点都是原点
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列条件中，能判定两个直角三角形全等的个数有_____个．①两条直角边对应相等；②斜边和一锐角对应相等；③斜边和一条直角边对应相等；④面积相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某学校学生的个性特长发展情况，在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目（每人只限一项）的情况．并将所得数据进行了统计，结果如图所示．
（1）求在这次调查中，一共抽查了多少名学生；
（2）求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数；
（3）若该校有2400名学生，请估计该校参加“美术”活动项目的人数
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，a，b，c分别为∠A，∠B，∠C所对的边，我们称关于x的一元二次方程
为“△ABC的☆方程”．根据规定解答下列问题：（1）“△ABC的☆方程”
的根的情况是______（填序号）：①有两个相等的实数根；②有两个不相等的实数根；③没有实数根；
（2）如图，AD为⊙O的直径，BC为弦， BC⊥AD于E，∠DBC=30°，求“△ABC的☆方程”
的解；
（3）若x=
是“△ABC的☆方程” 的一个根，其中a，b，c均为整数，且
，求方程的另一个根．
相关试题
