【题目】在直角坐标系xoy中,已知点P是反比例函数![]() 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
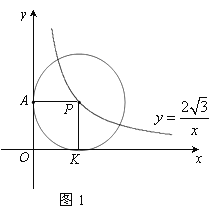
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
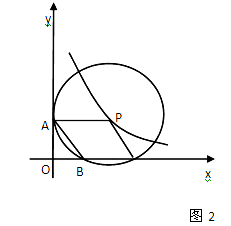
①求出点A,B,C的坐标.
②在P点右侧的反比例函数![]() 图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由.
图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由.
参考答案:
【答案】(1)四边形为正方形,理由见解析;(2)A(0,![]() ),B(1,0),C(3,0).M(
),B(1,0),C(3,0).M(![]() )
)
【解析】
试题分析:(1)根据AP、PK是圆的半径可得出AP=PK,再由![]() 轴,
轴,![]() 轴,
轴,![]() 可得出结论;
可得出结论;
(2)①连接PB,设点P(x,![]() ),过点P作
),过点P作![]() 与G,则半径
与G,则半径![]() ,有菱形的性质得
,有菱形的性质得![]() ,可知
,可知![]() 等边三角形,在
等边三角形,在![]() 中,
中,![]() ,PB=PA=x,
,PB=PA=x,![]() ,利用sin
,利用sin![]() ,列方程求x即可.
,列方程求x即可.
②先根据菱形的性质得出P点的坐标,再由待定系数法求出直线BP的解析式,设出M点的坐标,根据![]() 的面积等于菱形ABCP的面积得出m的值,进而可得出点M的坐标.
的面积等于菱形ABCP的面积得出m的值,进而可得出点M的坐标.
试题解析:
(1)四边形OKPA是正方形.
∵⊙P分别与两坐标轴相切,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴四边形OKPA是矩形.
∵AP=KP,
∴四边形OKPA是正方形.
(2)①连接PB,设点P的横坐标为x,则其纵坐标为![]() ,
,
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴![]() 为等边三角形.
为等边三角形.
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
![]() ,即
,即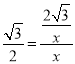 .
.
解得:![]() (负值舍去).
(负值舍去).
∴![]() ,
,![]() .
.
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3
∴可求得:A(0,![]() ),B(1,0) C(3,0).
),B(1,0) C(3,0).
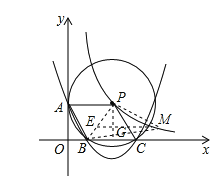
②利用B(1,0),P(2,![]() )易得BP: y=
)易得BP: y=![]() x-
x-![]()
过M作ME∥x轴,交线段BP于点E
设M(m,![]() ),则E(
),则E(![]() +1 ,
+1 ,![]() )
)
ME=m-![]() -1
-1
由MBP的面积=菱形ABCP的面积得:![]() (m-
(m-![]() -1)=
-1)=![]()
化简得![]() ,解得
,解得![]() (舍)
(舍)
所以M(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a <-1,则方程x2+(1-2a)x+a2=0根的情况是
A. 有两个不相等的实数根 B. 有两个相等的实根
C. 没有实数根 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a2>b2,则a>b”的逆命题是_____,该逆命题是(填“真”或“假”)_____命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明某学期的数学平时成绩70分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时:期中:期末=3:3:4,则小明总评成绩是________分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:① DF=CF;② BF⊥EN;③△BEN是等边三角形;④ S△BEF=3S△DEF. 其中,正确的结论有( )
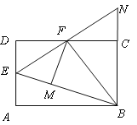
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2,y=-2x2,y=2x2+1共有的性质是
A. 开口向上 B. 对称轴都是y轴 C. 都有最高点 D. 顶点都是原点
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣33= .
相关试题

