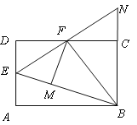
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:① DF=CF;② BF⊥EN;③△BEN是等边三角形;④ S△BEF=3S△DEF. 其中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】C
【解析】
试题分析:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,由折叠的性质可得:∠EMF=∠D=90°,DF=MF,
即FM⊥BE,CF⊥BC, ∵BF平分∠EBC, ∴CF=MF, ∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF, ∴∠BFM=∠BFC, ∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN, ∵∠BFE+∠BFN=180°, ∴∠BFE=90°, 即BF⊥EN,故②正确;
∵在△DEF和△CNF中,∠D=∠FCN=90°,DF=CF,∠DFE=∠CFN∴△DEF≌△CNF(ASA),
∴EF=FN, ∴BE=BN, 但无法求得△BEN各角的度数, ∴△BEN不一定是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF, ∴BM=BC=AD=2DE=2EM, ∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;∴④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a2>b2,则a>b”的逆命题是_____,该逆命题是(填“真”或“假”)_____命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明某学期的数学平时成绩70分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时:期中:期末=3:3:4,则小明总评成绩是________分.
-
科目: 来源: 题型:
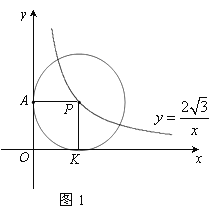
查看答案和解析>>【题目】在直角坐标系xoy中,已知点P是反比例函数
 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
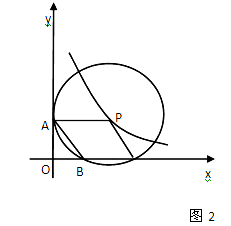
①求出点A,B,C的坐标.
②在P点右侧的反比例函数
 图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由.
图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2,y=-2x2,y=2x2+1共有的性质是
A. 开口向上 B. 对称轴都是y轴 C. 都有最高点 D. 顶点都是原点
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣33= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,能判定两个直角三角形全等的个数有_____个.①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一条直角边对应相等;④面积相等.
相关试题

