搜索
【题目】用同样大小的两种不同颜色的正方形纸片，按下图方式拼正方形．
第（1）个图形中有1个正方形；
第（2）个图形有1+3＝4个小正方形；
第（3）个图形有1+3+5＝9个小正方形
第（5）个图形有 个小正方形（直接写出结果）；
（1）根据上面的发现我们可以猜想：1+3+5+7+…+（2n﹣1）＝ （用含n的代数式表示）；
（2）请根据你的发现计算：①1+3+5+7+…+99＝ ；②101+103+105+…+199＝ ．
参考答案：
【答案】25；（1）n2；（2）①2500，②7500
【解析】
根据已知图形得出第2个图形比第1个图形多：4-1=3个；第3个图形比第2个图形多：9-4=5个；第4个图形比第3个图形多：16-9=7个；即可得出后面一个图形比前面一个图形多的个数是连续奇数，进而得出公式第n个图形比第（n-1）个图形多2n-1个小正方形；由此利用规律得出答案即可.
解：由题意得：第（5）个图形有：1+3+5+7+9＝25个小正方形；
（1）1+3＝4＝22，
1+3+5＝9＝32，
1+3+5+7＝16＝42，
…
∴1+3+5+7+…+（2n﹣1）＝
＝n2
（2）①1+3+5+7+…+99＝
＝502＝2500；
②∵1+3+5+…+199＝
＝10000，
1+3+5+7+…+99＝＝502＝2500，
∴101+103+105+…+199＝10000﹣2500＝7500．
故答案为：25，（1）n2，（2）①2500，②7500．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题：
（1）将下面的表格补充完整：
正多边形边数
3
4
5
6
…
n
∠α的度数
60°
45°
…
（2）根据规律，是否存在一个正多边形，其中的∠α＝21°？若存在，请求出n的值，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在航线l的两侧分别有观测点A和B，点B到航线l的距离BD为4km，点A位于点B北偏西60°方向且与B相距20km处．现有一艘轮船从位于点A南偏东74°方向的C处，沿该航线自东向西航行至观测点A的正南方向E处．求这艘轮船的航行路程CE的长度．（结果精确到0.1km）（参考数据：
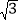≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49）
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读理解：如图1是二环三角形，可得S＝∠A1+∠A2+…+∠A6＝360°
理由：连接A1A4
∵∠1+∠2+∠A1OA4＝180°
∠A5+∠A6+∠A5OA6＝180°
又∵∠A1OA4＝∠A5OA6
∴∠1+∠2＝∠A5+∠A6
∴∠A2+∠3+∠1+∠2+∠4+∠A3＝360°
∴∠A2+∠3+∠A5+∠A6+∠4+∠A3＝360°
即S＝360°
（2）延伸探究：
①如图2是二环四边形，可得S＝∠A1+∠A2+…+∠A8＝720°，请你加以证明
②如图3是二环五边形，可得S＝ ，聪明的你，能根据以上的规律直接写出二环n边形（n≥3的整数）中，S＝ 度．（用含n的代数式表示最后的结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】
（发现）如图①，在△ABC中，点D，E分别是AB，AC的中点，可以得到：DE∥BC，且DE＝
BC．（不需要证明）
（探究）如图②，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，判断四边形EFGH的形状，并加以证明．
（应用）在（探究）的条件下，四边形ABCD中，满足什么条件时，四边形EFGH是菱形？你添加的条件是： ．（只添加一个条件）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD的边AB在x轴上，点C的坐标为（﹣5，4），点D在y轴的正半轴上，经过点A的直线y＝
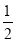x﹣1与y轴交于点E，将直线AE沿y轴向上平移n（n＞0）个单位长度后，得到直线l，直线l经过点C时停止平移．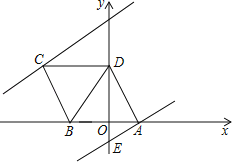
（1）点A的坐标为 ，点B的坐标为 ；
（2）若直线l交y轴于点F，连接CF，设△CDF的面积为S（这里规定：线段是面积为0的三角形），求S与n之间的函数关系式，并写出n的取值范围；
（3）易知AE⊥AD于点A,若直线l交折线AD﹣DC于点P，当△AEP为直角三角形时，请直接写出n的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．
（1）求证：AE=DF；
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
相关试题
