【题目】如图,平行四边形ABCD的边AB在x轴上,点C的坐标为(﹣5,4),点D在y轴的正半轴上,经过点A的直线y=![]() x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
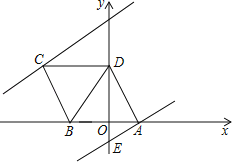
(1)点A的坐标为 ,点B的坐标为 ;
(2)若直线l交y轴于点F,连接CF,设△CDF的面积为S(这里规定:线段是面积为0的三角形),求S与n之间的函数关系式,并写出n的取值范围;
(3)易知AE⊥AD于点A,若直线l交折线AD﹣DC于点P,当△AEP为直角三角形时,请直接写出n的取值范围.
参考答案:
【答案】(1)A(2,0),B(-3,0);(2)当0≤n≤5时,S=10-2n;当5<n≤![]() 时,S=2n-10;(3)n=
时,S=2n-10;(3)n=![]() 或0≤n≤5.
或0≤n≤5.
【解析】
(1)令y=0,则![]() x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
(2)易求E(0,-1),当l到达C点时的解析式为y=![]() x+
x+![]() ,当0≤n≤5时,S=
,当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;当5<n≤
×4×(5-n)=10-2n;当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)由点可以得到AD⊥AE;当P在AD上时,△AEP为直角三角形,0≤n≤5;当P在CD上时,△AEP为直角三角形,则PE⊥AE,设P(m,4),可得![]() =-2,求出P(-
=-2,求出P(-![]() ,4),此时l的解析式为y=
,4),此时l的解析式为y=![]() x+
x+![]() ,则n=
,则n=![]() .
.
(1)令y=0,则![]() x-1=0,x=2,
x-1=0,x=2,
∴A(2,0),
∵C的坐标为(-5,4),四边形ABCD是平行四边形,
∴AB=CD=5,
∴OB=AB-OA=3,∴B(-3,0);
(2)当x=0时,y=![]() x﹣1=-1,所以E(0,-1),
x﹣1=-1,所以E(0,-1),
∵直线AE沿y轴向上平移得到l,当l到达C点时的解析式为y=![]() x+
x+![]() ,
,
此时l与y轴的交点为(0,![]() ),
),
当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;
×4×(5-n)=10-2n;
当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)∵D(0,4),A(2,0),E(0,-1),
∴AD=2![]() ,AE=
,AE=![]() ,ED=5,
,ED=5,
∴AD2+AE2=ED2,
∴AD⊥AE,
当P在AD上时,△AEP为直角三角形,
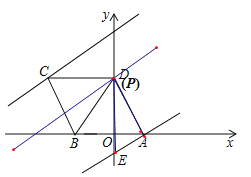
∴0≤n≤5;
当P在CD上时,△AEP为直角三角形,
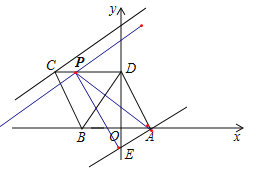
则PE⊥AE,
设P(m,4),
∴![]() =-2,
=-2,
∴m=-![]() ,
,
∴P(-![]() ,4),
,4),
∴此时l的解析式为y=![]() x+
x+![]() ,
,
∴n=![]() ;
;
综上所述:当△AEP为直角三角形时,n=![]() 或0≤n≤5.
或0≤n≤5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:如图1是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°
理由:连接A1A4
∵∠1+∠2+∠A1OA4=180°
∠A5+∠A6+∠A5OA6=180°
又∵∠A1OA4=∠A5OA6
∴∠1+∠2=∠A5+∠A6
∴∠A2+∠3+∠1+∠2+∠4+∠A3=360°
∴∠A2+∠3+∠A5+∠A6+∠4+∠A3=360°
即S=360°
(2)延伸探究:

①如图2是二环四边形,可得S=∠A1+∠A2+…+∠A8=720°,请你加以证明
②如图3是二环五边形,可得S= ,聪明的你,能根据以上的规律直接写出二环n边形(n≥3的整数)中,S= 度.(用含n的代数式表示最后的结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形
第(5)个图形有 个小正方形(直接写出结果);

(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)= (用含n的代数式表示);
(2)请根据你的发现计算:①1+3+5+7+…+99= ;②101+103+105+…+199= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(发现)如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=
 BC.(不需要证明)
BC.(不需要证明)
(探究)如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
(应用)在(探究)的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: .(只添加一个条件)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.

(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子顶端B到地面距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于4m,同时梯子的顶端B下降至B′,那么BB′的长为( )

A. 等于1mB. 大于1mC. 小于1mD. 以上答案都不对
相关试题

