Question

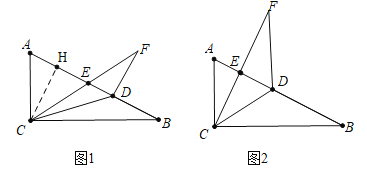
【题目】如图，在直角三角形纸片ABC中，∠ACB=90°，AC=2，BC=4，点D在边AB上，以CD为折痕将△CBD折叠得到△CPD，CP与边AB交于点E，若△DEP为直角三角形，则BD的长是_____

Answer 1

【答案】或2﹣2．

【解析】

分两种情形：①如图1中，当∠EDF=90°时，作CH⊥AB于H．只要证明CH=DH，即可解决问题；②如图2中，当∠DEF=90°时，设DE=x，则EF=2x，DF=BD=x，构建方程即可解决问题．

如图1中，当∠EDF=90°时，作CH⊥AB于H．

在Rt△ACB中，∵AC=2，BC=4，∴AB==2，∴CH==．

∵∠ACB=∠AHC=90°，∴∠ACH+∠BCH=90°，∠BCH+∠B=90°，∴∠ACH=∠B=∠F．

∵CH∥DF，∴∠F=∠HCE，∴∠ACH=∠HCE，∠DCE=∠DCB，∴∠HCD=45°，∴HC=HD=．

∵AH==，∴BD=AB﹣AH﹣DH=2﹣=．

如图2中，当∠DEF=90°时，设DE=x，则EF=2x，DF=BD=x．

∵AE+DE+BD=2，∴+x+x=2，∴x=2﹣，∴BD=x=2﹣2．

综上所述：BD的长为或2﹣2．

故答案为：或2﹣2．