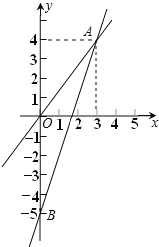
【题目】如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.

(1)求这两个函数的表达式;
(2)求△AOB的面积S.
参考答案:
【答案】(1)y=ax+b,y=3x﹣5;(2)![]()
【解析】
试题分析:(1)把A点坐标代入可先求得直线OA的解析式,可求得OA的长,则可求得B点坐标,可求得直线AB的解析式;
(2)由A点坐标可求得A到y轴的距离,根据三角形面积公式可求得S.
解:
(1)设直线OA的解析式为y=kx,
把A(3,4)代入得4=3k,解得k=![]() ,
,
所以直线OA的解析式为y=![]() x;
x;
∵A点坐标为(3,4),
∴OA=![]() =5,
=5,
∴OB=OA=5,
∴B点坐标为(0,﹣5),
设直线AB的解析式为y=ax+b,
把A(3,4)、B(0,﹣5)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=3x﹣5;
(2)∵A(3,4),
∴A点到y轴的距离为3,且OB=5,
∴S=![]() ×5×3=
×5×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列去括号中,正确的是( )
A. a2-(1-2a)=a2-1-2a B. a2+(-1-2a)=a2-l + 2a
C. a-[5b-(2c-1)]=a-5b+2c-1 D. -(a + b)+(c-d)=-a-b-c + d
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某一个顶点与和它不相邻的其他各顶点连接,可将多边形分成7个三角形,则这个多边形是( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
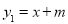 与
与 轴、
轴、 轴分别交于点
轴分别交于点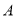 、
、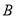 ,与双曲线
,与双曲线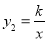 (
(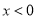 )分别交于点
)分别交于点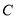 、
、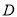 ,且
,且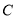 的坐标为(
的坐标为(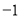 ,2).
,2).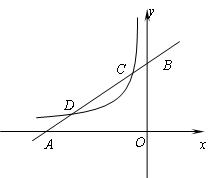
(1)分别求出直线
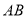 及双曲线的解析式;
及双曲线的解析式;(2)求出点
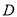 的坐标
的坐标(3)利用图象直接写出:不等式
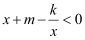 的解集
的解集 -
科目: 来源: 题型:
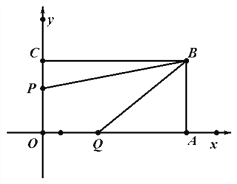
查看答案和解析>>【题目】如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)
(1)填空:点A的坐标为 ,点C的坐标为 ,点P的坐标为 (用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1 B.﹣3≤m≤1 C.﹣3≤m≤3 D.﹣1≤m≤0
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过连接对角线的方法,从一个顶点引出的对角线把十边形分成互不重叠的三角形的个数为( )
A. 7 B. 8 C. 9 D. 10
相关试题

