【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.

(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由OA=OD知∠OAD=∠ODA,由AD平分∠EAF知∠DAE=∠DAO,据此可得∠DAE=∠ADO,继而知OD∥AE,根据AE⊥EF即可得证;
(2)作OG⊥AE,知AG=CG=![]() AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
(1)如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠EAF,∴∠DAE=∠DAO,∴∠DAE=∠ADO,∴OD∥AE.
∵AE⊥EF,∴OD⊥EF,∴EF是⊙O的切线;
(2)如图,作OG⊥AE于点G,连接BD,则AG=CG=![]() AC=2,∠OGE=∠E=∠ODE=90°,∴四边形ODEG是矩形,∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°.
AC=2,∠OGE=∠E=∠ODE=90°,∴四边形ODEG是矩形,∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,∴△ADE∽△ABD,∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴AD2=48.在Rt△ABD中,BD=
,∴AD2=48.在Rt△ABD中,BD=![]() =4.在Rt△ABD中,∵AB=2BD,∴∠BAD=30°,∴∠BOD=60°,则
=4.在Rt△ABD中,∵AB=2BD,∴∠BAD=30°,∴∠BOD=60°,则![]() 的长度为
的长度为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形纸片ABC中,∠ACB=90°,AC=2,BC=4,点D在边AB上,以CD为折痕将△CBD折叠得到△CPD,CP与边AB交于点E,若△DEP为直角三角形,则BD的长是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】为规范学生的在校表现,某班实行了操行评分制,根据学生的操行分高低分为A、B、C、D四个等级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为_____人,得到等级A的学生人数在扇形统计图中的圆心角度数是_____;
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽到的代表中有小伟或小颖的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC中,点D在斜边BC上,以AD为直角边作等腰直角三角形ADE.

(1)求证:△ABD≌△ACE;
(2)求证:BD2+CD2=2AD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

-
科目: 来源: 题型:
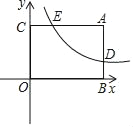
查看答案和解析>>【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=
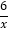 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
相关试题

