【题目】如图,根据要求回答下列问题:
(1)点A关于y轴对称点A′的坐标是 ;点B关于y轴对称点B′的坐标是
(2)作出△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
(3)求△ABC的面积.

参考答案:
【答案】(1)(3,2),(4,﹣3);(2)图形见解析(3)![]()
【解析】试题分析:
(1)对照图形可知点A、B的坐标分别:(-3,2)、(-4,-3),由此写出点A′、B′的坐标即可;
(2)分别作出点A、B、C关于y轴的对称点A′、B′、C′,再顺次连接这三点即可得到所求三角形;
(3)如图,由S△ABC=S矩形DBEF-S△ADB-S△BEC-S△AFC,计算出△ABC的面积即可.
试题解析:
(1)由图可知:点A、B的坐标分别:(-3,2)、(-4,-3),
∴点A、B关于y轴的对称点A′和B′的坐标分别为:(3,2),(4,﹣3);
(2)如下图所示;△A′B′C′为所求的图形;

(3)如图:
S△ABC=S矩形DBEF-S△ADB-S△BEC-S△AFC
=![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此规律,将△OAB进行n次变换,得到△OAnBn。推测An的坐标是___________,Bn的坐标是___________。( )

A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,建立如图所示的直角坐标系,已知两点A(0,2),B(4,1)

(1)请在x轴上画出一点P,使得PA+PB的值最小;
(2)请直接写出:点P的坐标 ;PA+PB的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
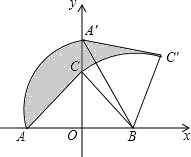
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动点A在函数y=
 (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.

(1)求这两个函数的表达式;
(2)求△AOB的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形纸片ABC中,∠ACB=90°,AC=2,BC=4,点D在边AB上,以CD为折痕将△CBD折叠得到△CPD,CP与边AB交于点E,若△DEP为直角三角形,则BD的长是_____

相关试题

