【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=![]() (x<0)的图象经过AO的中点C,交AB于点D.若点D的坐标为(﹣4,n),且AD=3.
(x<0)的图象经过AO的中点C,交AB于点D.若点D的坐标为(﹣4,n),且AD=3.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求经过C、D两点的直线所对应的函数解析式;
(3)设点E是线段CD上的动点(不与点C、D重合),过点E且平行y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.

参考答案:
【答案】(1)y=﹣![]() ;y=
;y=![]() x+3;(3)如m=﹣3时,S△OEF最大,最大值为
x+3;(3)如m=﹣3时,S△OEF最大,最大值为![]()
【解析】
(1)先确定出点A坐标,进而得出点C坐标,将点C,D坐标代入反比例函数中即可得出结论;
(2)由n=1,求出点C,D坐标,利用待定系数法即可得出结论;
(3)设出点E坐标,进而表示出点F坐标,即可建立面积与m的函数关系式即可得出结论.
(1)∵AD=3,D(﹣4,n),
∴A(﹣4,n+3),
∵点C是OA的中点,
∴C(﹣2,![]() ),
),
∵点C,D(﹣4,n)在双曲线y=![]() 上,
上,
∴ ,
,
∴![]() ,
,
∴反比例函数解析式为y=﹣![]() ;
;
②由①知,n=1,
∴C(﹣2,2),D(﹣4,1),
设直线CD的解析式为y=ax+b,
∴![]() ,
,
∴ ,
,
∴直线CD的解析式为y=![]() x+3;
x+3;
(3)如图,由(2)知,直线CD的解析式为y=![]() x+3,
x+3,
设点E(m,![]() m+3),
m+3),
由(2)知,C(﹣2,2),D(﹣4,1),
∴﹣4<m<﹣2,
∵EF∥y轴交双曲线y=﹣![]() 于F,
于F,
∴F(m,﹣![]() ),
),
∴EF=![]() m+3+
m+3+![]() ,
,
∴S△OEF=![]() (
(![]() m+3+
m+3+![]() )×(﹣m)=﹣
)×(﹣m)=﹣![]() (
(![]() m2+3m+4)=﹣
m2+3m+4)=﹣![]() (m+3)2+
(m+3)2+![]() ,
,
∵﹣4<m<﹣2,
∴m=﹣3时,S△OEF最大,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )

A. AD=CE B. MF=
 CF C. ∠BEC=∠CDA D. AM=CM
CF C. ∠BEC=∠CDA D. AM=CM -
科目: 来源: 题型:
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:
 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
 ≈1.73.)
≈1.73.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,∠ABC=45°,BE⊥AC于点E,AD⊥BC于点D,BE与AD相交于F.

(1)求证:BF=AC;
(2)若BF=3,求CE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边 且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲
乙
进价(元/部)
4000
2500
售价(元/部)
4300
3000
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于
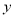 轴对称的
轴对称的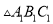 ,并写出
,并写出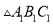 三个顶点的坐标:
三个顶点的坐标: 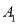 ( ),
( ), ( ),
( ), ( );
( );(2)直接写出△ABC的面积为 ;
(3)在
 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.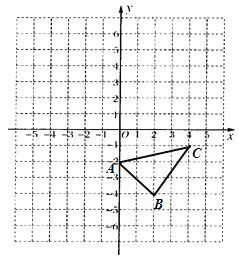
相关试题

