【题目】如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交于点P,则∠BPC=°. 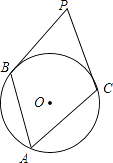
参考答案:
【答案】70
【解析】解:连接OB,OC, ∵PB,PC是⊙O的切线,
∴OB⊥PB,OC⊥PC,
∴∠PBO=∠PCO=90°,
∵∠BOC=2∠BAC=2×55°=110°,
∴∠BPC=360°﹣∠PBO﹣∠BOC﹣∠PCO=360°﹣90°﹣110°﹣90°=70°.
所以答案是:70.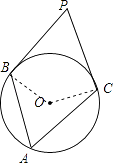
【考点精析】本题主要考查了圆周角定理和切线的性质定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?
解:,
根据题意,得x2x=288.
解这个方程,得x1=﹣12(不合题意,舍去),x2=12
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2 .我的结果也正确!
(1)小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?
(2)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样…
(3)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角, ①若AB是⊙O的直径,则∠APB=°;②若⊙O的半径是1,AB= ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )

A. +1
+1
B. +1
+1
C.2.5
D.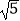
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(1+
 )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
 x﹣1>2x,并把解集在数轴上表示出来.
x﹣1>2x,并把解集在数轴上表示出来. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
组别
垫球个数x(个)
频数(人数)
频率
1
10≤x<20
5
0.10
2
20≤x<30
a
0.18
3
30≤x<40
20
b
4
40≤x<50
16
0.32
合计
1
(1)表中a= , b=;
(2)这个样本数据的中位数在第组;
(3)下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人? 排球30秒对墙垫球的中考评分标准分值
10
9
8
7
6
5
4
3
2
1
排球(个)
40
36
33
30
27
23
19
15
11
7
相关试题

