【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2? |
我的结果也正确!
(1)小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?
(2)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样…
(3)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 

参考答案:
【答案】
(1)设矩形蔬菜种植区域的宽为xm,则长为2xm
(2)解:小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由.
在“设矩形蔬菜种植区域的宽为x m,则长为2x m.”前补充以下过程:
设温室的宽为x m,则长为2x m.
则矩形蔬菜种植区域的宽为(x﹣1﹣1)m,长为(2x﹣3﹣1)m.
∵ ![]() ,
,
∴矩形蔬菜种植区域的长与宽之比为2:1
(3)解:要使矩形A′B′C′D′∽矩形ABCD,
就要 ![]() ,即
,即 ![]() ,
,
即 ![]() ,
,
即2AB﹣2(b+d)=2AB﹣(a+c),
∴a+c=2(b+d),
即 ![]() .
.

【解析】(2)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得 ![]() ,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(3)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得
,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(3)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得 ![]() ,即
,即 ![]() ,然后利用比例的性质,即可求得答案.
,然后利用比例的性质,即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图说故事. 请你编写一个故事,使故事情境中出现的一对变量x、y满足图示的函数关系,要求:

(1)指出变量x和y的含义;
(2)利用图中的数据说明这对变量变化过程的实际意义,其中须涉及“速度”这个量. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的和为42,则这9个数的和为( )

A. 69 B. 84 C. 189 D. 207
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm.

(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2 , 当⊙O1的半径为多少时,该玩具的制作成本最小? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角, ①若AB是⊙O的直径,则∠APB=°;②若⊙O的半径是1,AB= ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )

A. +1
+1
B. +1
+1
C.2.5
D.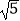
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交于点P,则∠BPC=°.
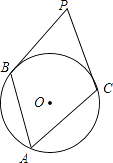
相关试题

