【题目】(12分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
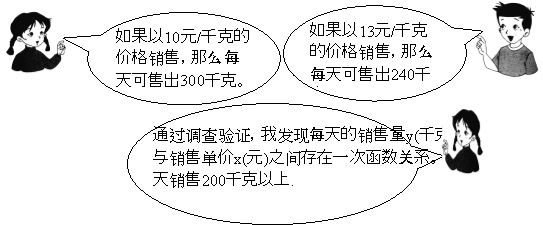
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式。(6分)
(2)该超市销售这种水果每天获取的利润为1040元,那么销售单价为多少元?(6分)
参考答案:
【答案】(1)y=-20x+500,(2)12,21(舍去)
【解析】
试题分析:(1)因为y是x的一次函数,所以设y=kx+b,把x=10,y=300;x=11,y=250代入,然后解方程组即可得到k,b,从而得出y(千克)与x(元)(x>0)的函数关系式;(2)根据每天获取的利润=每千克的利润×每天的销售量得到方程:(x-8)(-50x+800)=1040,然后解方程即可.
试题解析:(1)因为y是x的一次函数,所以设y=kx+b,
∵x=10,y=300;x=13,y=240,
∴![]() ,解得
,解得![]() ,
,
∴y=﹣20x+500,
(2)根据题意可得:(x﹣8)y=1040,所以(x-8)(-50x+800)=1040,解得x=12或x=21,因为要保证每天销售200千克以上,所以x=21不合题意舍去,所以x=12,
答:销售单价为12元.
-
科目: 来源: 题型:
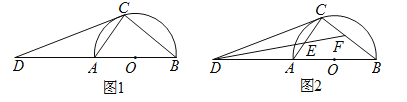
查看答案和解析>>【题目】如图
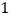 ,
, 为半圆
为半圆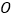 的直径,
的直径,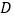 为
为 的延长线上一点,
的延长线上一点,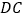 为半圆
为半圆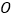 的切线,切点为
的切线,切点为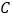 .
.
(
 )求证:
)求证: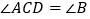 .
.(
 )如图
)如图 ,
,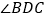 的平分线分别交
的平分线分别交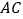 ,
,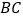 于点
于点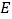 ,
,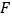 ,求
,求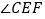 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知直线
 直线
直线 和直线
和直线 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线
 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上的动点,若在边AC,BC上分别有点E,F,使得
AE=AD,BF=BD.
(1)设∠C=α,求∠EDF(用含α的代数式表示);
(2)尺规作图:分别在边AB,AC上确定点P,Q(PQ不与DE平行或重合),使得
∠CPQ=∠EDF.(保留作图痕迹,不写作法)

-
科目: 来源: 题型:
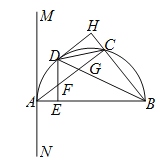
查看答案和解析>>【题目】如图,
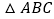 内接于半圆,
内接于半圆,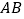 是直径,过
是直径,过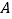 作直线
作直线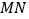 ,
,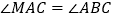 ,
,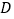 是弧
是弧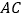 的中点,连接
的中点,连接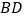 交
交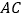 于
于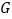 ,过
,过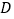 作
作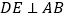 于
于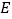 ,交
,交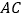 于
于 .
.
(
 )求证:
)求证: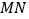 是半圆的切线.
是半圆的切线.(
 )作
)作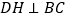 交
交 的延长线于点
的延长线于点 ,连接
,连接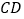 ,试判断线段
,试判断线段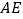 与线段
与线段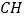 的数量关系,并说明理由.
的数量关系,并说明理由.(
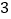 )若
)若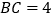 ,
,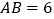 ,试求
,试求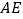 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E.则AD与BE平行吗?
完成下面的解答过程(填写理由或数学式).
解:∵∠1=∠2(已知),
∴ ∥ (内错角相等,两直线平行),
∴∠E=∠ (两直线平行,内错角相等),
又∵∠E=∠3(已知),
∴∠3=∠ (等量代换),
∴AD∥BE( ).

相关试题

