【题目】如图,![]() 内接于半圆,
内接于半圆,![]() 是直径,过
是直径,过![]() 作直线
作直线![]() ,
,![]() ,
,![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
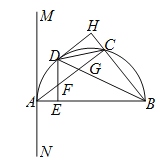
(![]() )求证:
)求证:![]() 是半圆的切线.
是半圆的切线.
(![]() )作
)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() ,
,![]() ,试求
,试求![]() 的长.
的长.
参考答案:
【答案】(1)答案见解析;(2)AE=CH;(3)1.
【解析】试题分析:(1)由AB是直径得出∠ACB=90°,推出∠CAB+∠MAC=90°即可;
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
试题解析:解:(1)如图所示.∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°.∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,即∠MAB=90°,∴MN是半圆的切线;

(2)AE=CH.理由如下:
连接AD.∵D是弧AC的中点,∴AD=CD,∠HBD=∠ABD.∵DE⊥AB,DH⊥BC,∴DE=DH,∠AED=∠DHC,在Rt△ADE和Rt△CDH中,∵AD=CD,DE=DH,∴Rt△ADE≌Rt△CDH(HL),∴AE=CH;

(3)由(2)知DH=DE,∠DHB=∠DEB=90°,在Rt△DBH和Rt△DBE中,∵DH=DE,BD=BD,∴Rt△DBH≌Rt△DBE(HL),∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,又∵AB=6,BC=4,∴6﹣AE=4+AE,∴AE=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
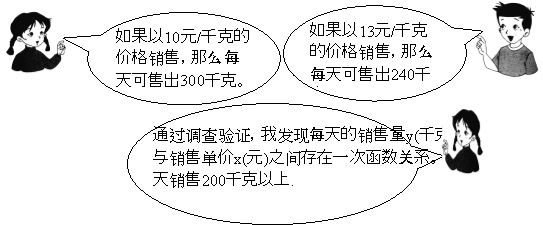
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式。(6分)
(2)该超市销售这种水果每天获取的利润为1040元,那么销售单价为多少元?(6分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上的动点,若在边AC,BC上分别有点E,F,使得
AE=AD,BF=BD.
(1)设∠C=α,求∠EDF(用含α的代数式表示);
(2)尺规作图:分别在边AB,AC上确定点P,Q(PQ不与DE平行或重合),使得
∠CPQ=∠EDF.(保留作图痕迹,不写作法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E.则AD与BE平行吗?
完成下面的解答过程(填写理由或数学式).
解:∵∠1=∠2(已知),
∴ ∥ (内错角相等,两直线平行),
∴∠E=∠ (两直线平行,内错角相等),
又∵∠E=∠3(已知),
∴∠3=∠ (等量代换),
∴AD∥BE( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,一次函数
,一次函数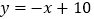 的图像交
的图像交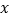 轴于点
轴于点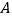 ,交
,交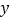 轴于点
轴于点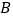 .以
.以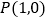 为圆心的⊙
为圆心的⊙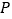 与
与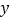 轴相切,若点
轴相切,若点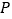 以每秒
以每秒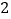 个单位的速度沿
个单位的速度沿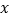 轴向右平移,同时⊙
轴向右平移,同时⊙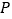 的半径以每秒增加
的半径以每秒增加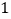 个单位的速度不断变大,设运动时间为
个单位的速度不断变大,设运动时间为 .
.(
 )点
)点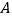 的坐标为__________,点
的坐标为__________,点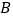 的坐标为__________,
的坐标为__________,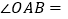 __________
__________ .
.(
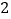 )在运动过程中,点
)在运动过程中,点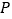 的坐标为__________,⊙
的坐标为__________,⊙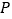 的半径为__________(用含
的半径为__________(用含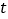 的代数式表示).
的代数式表示).(
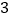 )当⊙
)当⊙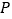 与直线
与直线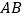 相交于点
相交于点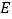 、
、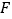 时.
时.①如图
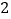 ,求
,求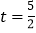 时弦
时弦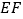 的长.
的长.②在运动过程中,是否存在以点
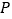 为直角顶点的
为直角顶点的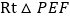 ,若存在,请求出
,若存在,请求出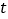 的值;若不存在,请说明理由(利用图
的值;若不存在,请说明理由(利用图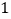 解题).
解题).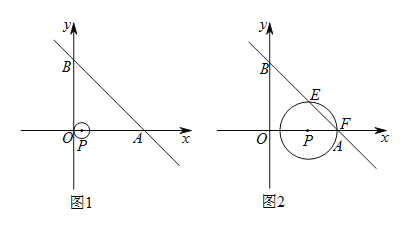
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
相关试题

