【题目】如图已知直线![]() 直线
直线![]() 和直线
和直线![]() 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.
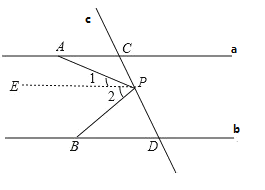
(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线![]() 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。

参考答案:
【答案】(1)∠APB=∠CAP+∠DBP;(2)不发生变化;(3)当P点在DC延长线上时:∠APB=∠DBP-∠CAP;当P点在CD延长线上时:∠APB=∠CAP-∠DBP
【解析】
(1)过点P作EP∥a,根据平行线的性质即可求解;
(2)根据平行线的性质可知不会发生变化;
(3)根据题意作出图形,根据平行线的性质即可求解.
(1)如图,过点P作EP∥a,
∵![]()
∴EP∥a∥b,
∴∠CAP=∠1,∠DBP=∠2,
∵∠APB=∠1+∠2,
∴∠APB=∠CAP+∠DBP
(2)当P点在C、D之间运动时,∠APB=∠CAP+∠DBP,不会发生变化;
(3)如图②,当P点在DC延长线上时:∠APB=∠DBP-∠CAP.
理由如下:
∵a∥b,∴∠PEC=∠PBD,
∵∠PEC=∠CAP +∠APB
∴∠PBD=∠CAP +∠APB
即∠APB=∠DBP-∠CAP.
如图③当P点在CD延长线上时:∠APB=∠CAP-∠DBP
理由如下:
∵a∥b,∴∠CAP =∠DEP,
∵∠DEP =∠DBP +∠APB
∴∠CAP =∠DBP +∠APB
即∠APB=∠CAP-∠DBP
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0),与函数y=x的图象交于点E,点E的横坐标为3.
(1)求函数y=kx+b的表达式;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=kx+b的图象和函数y=x的图象于点C,D,若四边形OBDC是平行四边形,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到
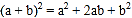 这个等式,请解答下列问题:
这个等式,请解答下列问题:
(1)写出图2中所表示的数学等式______________;(最后结果)
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值;
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+2b)(3a+5b)的长方形,求x+y+z的值.
-
科目: 来源: 题型:
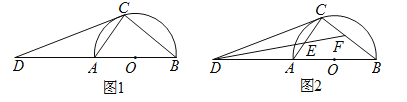
查看答案和解析>>【题目】如图
 ,
, 为半圆
为半圆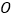 的直径,
的直径,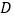 为
为 的延长线上一点,
的延长线上一点,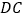 为半圆
为半圆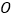 的切线,切点为
的切线,切点为 .
.
(
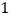 )求证:
)求证: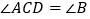 .
.(
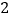 )如图
)如图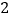 ,
,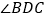 的平分线分别交
的平分线分别交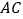 ,
,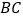 于点
于点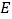 ,
,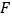 ,求
,求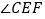 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
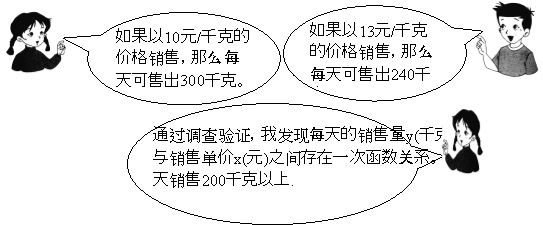
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式。(6分)
(2)该超市销售这种水果每天获取的利润为1040元,那么销售单价为多少元?(6分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上的动点,若在边AC,BC上分别有点E,F,使得
AE=AD,BF=BD.
(1)设∠C=α,求∠EDF(用含α的代数式表示);
(2)尺规作图:分别在边AB,AC上确定点P,Q(PQ不与DE平行或重合),使得
∠CPQ=∠EDF.(保留作图痕迹,不写作法)

相关试题

