搜索
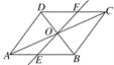
【题目】如图，在平行四边形ABCD中，对角线AC，BD交于点O，经过点O的直线交AB于E，交CD于F，AB＝4，AD＝3，OF＝1.3.求四边形BCFE的周长．
参考答案：
【答案】四边形BCFE的周长为9.6.
【解析】
直接利用平行四边形的性质结合全等三角形的判定与性质进而得出FO=EO=1.3，FC=AE，得出四边形BCFE的周长为：BC+EF+AB，进而求得问题的解．
解 ∵四边形ABCD是平行四边形，
∴AO＝CO，DC∥AB，
∴∠FCO＝∠EAO，
在△OFC和△OEA中
∵
∴△OFC≌△OEA(ASA)，
∴FO＝EO＝1.3，FC＝AE，
∴AE＋BE＝FC＋BE＝AB＝4，
∴四边形BCFE的周长为BC＋EF＋AB＝3＋4＋2.6＝9.6.
-
科目： 来源： 题型：
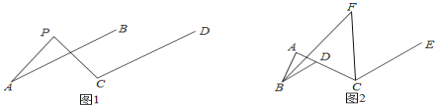
查看答案和解析>>【题目】如图1，已知AB∥CD，那么图1中∠PAB、∠APC、∠PCD之间有什么数量关系？并说明理由．
如图2，已知∠BAC＝80°，点D是线段AC上一点，CE∥BD，∠ABD和∠ACE的平分线交于点F，请利用（1）的结论求图2中∠F的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某公路检测中心在一事故多发地带安装了一个测速仪，检测点设在距离公路10m的A处，测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°，∠C=45°
（1）求B，C之间的距离；（保留根号）
（2）如果此地限速为80km/h，那么这辆汽车是否超速？请说明理由.（参考数据：
,
） -
科目： 来源： 题型：
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒售价比乙种羽毛球每筒的售价多15元，健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球，共花费255元．
（1）该网店甲、乙两种羽毛球每筒的售价各是多少元？
（2）根据健民体育活动中心消费者的需求量，活动中心决定用不超过2625元钱购进甲、乙两种羽毛球共50筒，那么最多可以购进多少筒甲种羽毛球？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AB=6，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点C1处，连接C1B，则BC1的最小值为（ ）
A.2
B.3
C.3
D.2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中
（1）写出点A，B，C的坐标．
（2）作出△ABC关于y轴的对称图形△A1B1C1．
（3）写出点A1，B1，C1的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=2，BC=4，点M、N分别在边AD和BC上，沿MN折叠四边形ABCD，使点A、B分别落在A1、B1处，得四边形A1B1NM，其中点B1在DC上，过点M作ME⊥BC于点E，连接BB1 ， 给出下列结论：①∠MNB1=∠ABB1；②△MEN∽△BCB1；③
的值为定值；④当B1C= 
DC时，AM= 
，其中正确结论的序号是 ． （把所有正确结论的序号都在填在横线上） 
相关试题
