【题目】如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1 , 给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③ ![]() 的值为定值;④当B1C=
的值为定值;④当B1C= ![]() DC时,AM=
DC时,AM= ![]() ,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上)
,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上) 
参考答案:
【答案】①②③
【解析】解:由折叠可知∠MNB1=∠BNM,MN⊥BB1,
∴∠BNM+∠B1BN=90°,
∵∠ABB1+∠B1BN=90°,
∴∠BNM=∠ABB1,
∴∠MNB1=∠ABB1,故①正确;
∵ME⊥BC,
∴∠MNE+∠NME=90°,
由由折叠的性质可得MN⊥BB1,
∴∠MNE+∠B1BN=90°,
∴∠NME=∠BB1N,
∴△MEN∽△BCB1,
故②正确;
由②可知 ![]() =
= ![]() ,
,
∵ME=AB=2,BC=4,
∴ ![]() =
= ![]() =
= ![]() ,为定值,故③正确;
,为定值,故③正确;
∵△MEN∽△BCB1,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴NE= ![]() B1C,
B1C,
若B1C= ![]() DC,
DC,
则NE= ![]() DC=
DC= ![]() ×2=
×2= ![]() ,
,
设BN=x,则NC=4﹣x,B1N=x,
在Rt△B1NC中,由勾股定理可得x2=(4﹣x)2+12,
解得x= ![]() ,
,
∴AM=BE=BN﹣NE= ![]() ﹣
﹣ ![]() =
= ![]() ,故④不正确.
,故④不正确.
所以答案是:①②③.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
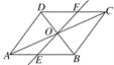
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F,AB=4,AD=3,OF=1.3.求四边形BCFE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )

A.2
B.3
C.3
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中
(1)写出点A,B,C的坐标.
(2)作出△ABC关于y轴的对称图形△A1B1C1.
(3)写出点A1,B1,C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有3个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2
 +2,则∠BAD的度数等于( )
+2,则∠BAD的度数等于( )
A. 120° B. 135° C. 150° D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出BE的长度.

相关试题

