【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
参考答案:
【答案】(1)(10![]() +10)m;(2)超速.
+10)m;(2)超速.
【解析】
试题分析:(1)利用∠B=30°,∠C=45°,AD=10,求出BD=10![]() ,DC=10,从而得出BC=10
,DC=10,从而得出BC=10![]() +10
+10
(2)利用![]() ,
,![]() ,求出BC
,求出BC![]() 27,再求出v=108千米/小时>80千米/小时,故超速。
27,再求出v=108千米/小时>80千米/小时,故超速。
试题解析:(1)如图,过点A作AD⊥BC于点D,则AD=10m
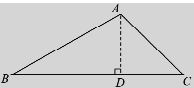
∵在RtΔACD中,∠C=45°
∴RtΔACD是等腰直角三角形
∴CD=AD=10m
在RtΔABD中,tanB=![]()
∵∠B=30°
∴![]()
∴BD=10![]() m
m
∴BC=BD+DC=(10![]() +10)m
+10)m
(2)这辆汽车超速.理由如下.
由(1)知BC=(10![]() +10)m,又
+10)m,又![]()
∴BC=27m
∴汽车速度v=![]() =30(m/s)
=30(m/s)
又30 m/s=108km/h,此地限速为80 km/h
∵108>80
∴这辆汽车超速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+2mx+9是完全平方式,则m的值为( )
A.6
B.±6
C.3
D.±3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a,b的单项式3am+2b3和-2a5bn+1是同类项,则m+n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数
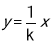 与
与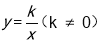 的图象性质.小明根据学习函数的经验,对函数
的图象性质.小明根据学习函数的经验,对函数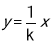 与
与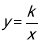 ,当k>0时
,当k>0时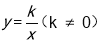 的图象性质进行了探究,下面是小明的探究过程:
的图象性质进行了探究,下面是小明的探究过程:(1)如图所示,设函数
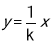 与
与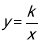 图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .(2)若P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下:设P(m,
 ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).则
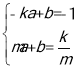 解得
解得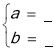
所以,直线PA的解析式为 .
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断ΔPAB的形状,并用k表示出ΔPAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】钟面角是指在钟表面上时针与分针所形成的夹角,6:20时钟面角的度数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB∥x轴,且AB=4,若点A的坐标为(﹣1,2),则点B的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动中,共募得捐款32000000元,将32000000用科学记数法表示为( )
A.0.32×108
B.3.2×106
C.3.2×107
D.32×106
相关试题

