【题目】如图,在平面直角坐标系中
(1)写出点A,B,C的坐标.
(2)作出△ABC关于y轴的对称图形△A1B1C1.
(3)写出点A1,B1,C1的坐标.

参考答案:
【答案】(1)A(﹣1,5),B(﹣1,0),C(﹣4,3);(2)画图见解析;(3) A1(1,5),B1(1,0),C1(4,3).
【解析】
(1)根据平面直角坐标系可得点A,B,C的坐标,注意书写点的坐标时,横坐标在前,纵坐标在后;
(2)首先确定A、B、C三点关于y轴的对称点的位置,然后再顺次连接即可;
(3)根据关于y轴对称点的坐标特点可得点A1,B1,C1的坐标.
解:(1)A(﹣1,5),B(﹣1,0),C(﹣4,3);
(2)如图所示:
(3)A1(1,5),B1(1,0),C1(4,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2625元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F,AB=4,AD=3,OF=1.3.求四边形BCFE的周长.
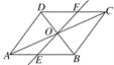
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )

A.2
B.3
C.3
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1 , 给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③
 的值为定值;④当B1C=
的值为定值;④当B1C=  DC时,AM=
DC时,AM=  ,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上)
,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有3个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB⊥BC,AB∥DC,AB,BC,CD分别为2,2,2
 +2,则∠BAD的度数等于( )
+2,则∠BAD的度数等于( )
A. 120° B. 135° C. 150° D. 以上都不对
相关试题

