【题目】如图,已知抛物线y=x2+bx+c与直线y=﹣x+3相交于坐标轴上的A,B两点,顶点为C.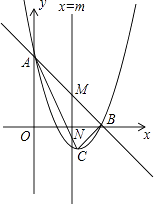
(1)填空:b= , c=;
(2)将直线AB向下平移h个单位长度,得直线EF.当h为何值时,直线EF与抛物线y=x2+bx+c没有交点?
(3)直线x=m与△ABC的边AB,AC分别交于点M,N.当直线x=m把△ABC的面积分为1:2两部分时,求m的值.
参考答案:
【答案】
(1)﹣4,3
(2)解:∵将直线AB:y=﹣x+3向下平移h个单位长度,得直线EF,
∴可设直线EF的解析式为y=﹣x+3﹣h.
把y=﹣x+3﹣h代入y=x2﹣4x+3,得x2﹣4x+3=﹣x+3﹣h.
整理得:x2﹣3x+h=0.
∵直线EF与抛物线没有交点,
∴△=(﹣3)2﹣4×1×h=9﹣4h<0,
解得h> ![]() .
.
∴当h> ![]() 时,直线EF与抛物线没有交点;
时,直线EF与抛物线没有交点;
(3)解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点C(2,﹣1).
设直线AC的解析式为y=mx+n.
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣2x+3.
如图,设直线AC交x轴于点D,则D( ![]() ,0),BD=
,0),BD= ![]() .
.
∴S△ABC=S△ABD+S△BCD= ![]() ×
× ![]() ×3+
×3+ ![]() ×
× ![]() ×1=3.
×1=3.
∵直线x=m与线段AB、AC分别交于M、N两点,则0≤m≤2,
∴M(m,﹣m+3),N(m,﹣2m+3),
∴MN=(﹣m+3)﹣(﹣2m+3)=m.
∵直线x=m把△ABC的面积分为1:2两部分,
∴分两种情况讨论:
①当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±
,解得 m=± ![]() ;
;
②当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±2
,解得 m=±2
∵0≤m≤2,
∴m= ![]() 或m=2.
或m=2.
∴当m= ![]() 或2时,直线x=m把△ABC的面积分为1:2两部分.
或2时,直线x=m把△ABC的面积分为1:2两部分.
【解析】解:(1)∵直线y=﹣x+3交坐标轴于A,B两点,
∴A(0,3),B(3,0),
把A(0,3),B(3,0)代入y=x2+bx+c,
得 ![]() ,解得
,解得 ![]() .
.
所以答案是﹣4,3;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
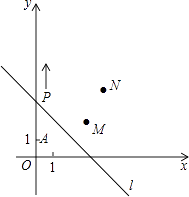
(1)当t=2时,则AP= , 此时点P的坐标是 .
(2)当t=3时,求过点P的直线l:y=﹣x+b的解析式?
(3)当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形
 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点 ,点
,点 ,动点
,动点 从
从 出发,沿
出发,沿 以每秒
以每秒 个单位的速度运动,同时,动点
个单位的速度运动,同时,动点 从
从 出发,沿
出发,沿 以每秒
以每秒 个单位的速度运动.当其中一点到达
个单位的速度运动.当其中一点到达 点时,两动点同时停止运动设运动时间为
点时,两动点同时停止运动设运动时间为 .
.
(1)当
 ______时,点
______时,点 追上点
追上点 ,此时点
,此时点 的坐标为_______.
的坐标为_______.(2)当
 时,分别取
时,分别取 、
、 的中点
的中点 、
、 ,如果四边形
,如果四边形 的面积等于
的面积等于 ,请求出时间
,请求出时间 的取值;
的取值;(3)如图2,连接
 ,已知
,已知 ,在(2)问的条件下,过点
,在(2)问的条件下,过点 作
作 于点
于点 ,问在长方形
,问在长方形 的四条边上是否存在点
的四条边上是否存在点 ,使得线段
,使得线段 ,若存在,请直接写出点
,若存在,请直接写出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
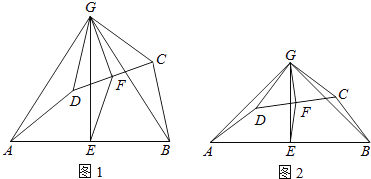
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求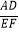 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A.2种B.3种C.4种D.5种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究
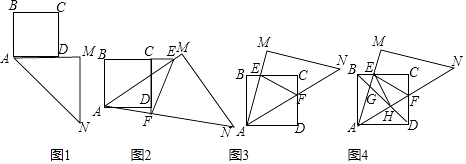
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.
相关试题

