【题目】如图①所示,ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 km2;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.

参考答案:
【答案】(1)0.48;(2)0.12km2;(3)(![]() +5)万元.
+5)万元.
【解析】
(1)过点B作BE⊥OA于点E,由平行四边形的性质得出AB=BO=0.5km,AO=0.6km,运用勾股定理求出BE的长,再运用三角形面积公式求出△AOB的面积,再乘以4即可得解;
(2)连接AM、CN,得出S△AMN=![]() SABCD,由平行四边形ABCD的面积为0.48km2可得结果;
SABCD,由平行四边形ABCD的面积为0.48km2可得结果;
(3)将AN沿MN向下平移0.5km至PM,连接PC交BD于点M',此时点N位于N'处,此时即为AN+CM=PC取最小值,过M作MG⊥AC于点G,证明四边形APM'N'和四边形AM'CN'均为平行四边形,得到PC=2M'C,求出MC=![]() 可得PC的值, 从而得AN、MN、CM和的最小值为:(
可得PC的值, 从而得AN、MN、CM和的最小值为:(![]() +0.5)km,再乘以每千米的费用即可得到答案.
+0.5)km,再乘以每千米的费用即可得到答案.
∵四边形ABCD是平行四边形,AC=1.2km,BD=1km,
∴OA=OC=![]() AC=0.6km,OB=OD=
AC=0.6km,OB=OD=![]() BD=0.5km,
BD=0.5km,
∴在△AOB中,过点B作BE⊥OA于点E,如图:

∵AB=OB=0.5km,OA=0.6km,BE⊥OA,
∴AE=![]() OA=0.3km,
OA=0.3km,
∴BE=![]() =0.4km,
=0.4km,
∴S△AOB=![]() OABE=
OABE=![]() ×0.6×0.4=0.12km2,
×0.6×0.4=0.12km2,
∴SABCD=4S△AOB=4×0.12=0.48km2;
∴公园的面积为0.48km2.
故答案为:0.48.
(2)连接AM、CN,如图:

∵在△ACM中,OA=OC,
∴S△COM=S△AOM,
∴S△AON+S△COM=S△AON+S△AOM=S△AMN.
∵OB=BM+MO,BM=ON,OB=OD=![]() BD,
BD,
∴MN=MO+ON=OB=![]() BD,
BD,
∴S△AMN=![]() SABCD=0.12km2,
SABCD=0.12km2,
∴S△AON+S△COM=S△AMN=0.12km2,
∴种植郁金香区域的面积为0.12km2.
(3)将AN沿MN向下平移0.5km至PM,连接PC交BD于点M',此时点N位于N'处,此时即为AN+CM=PC取最小值,过M'作M'G⊥AC于点G,如图:

∵MN=![]() BD=0.5km,AP∥M'N',AN'∥PC,
BD=0.5km,AP∥M'N',AN'∥PC,
∴OM'为△APC的中位线,
∴OM'=![]() AP=
AP=![]() M'N'=ON'=
M'N'=ON'=![]() km,
km,
∴四边形APM'N'和四边形AM'CN'均为平行四边形,
∴PC=2M'C,
由图①及BE=0.4km,OB=0.5km可知,sin∠BOA=![]() ,cos∠BOA=
,cos∠BOA=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在Rt△M'GC中,由勾股定理得: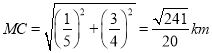 ,
,
∴PC=![]() km,
km,
∴AN、MN、CM和的最小值为:(![]() +0.5)km,
+0.5)km,
∴投入资金的最小值为:10×(![]() +0.5)=(
+0.5)=(![]() +5)(万元).
+5)(万元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3
 ,BC=7,求线段BD的长.
,BC=7,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A.B两种型号车的进货和销售价格如表,问应如何进货才能使这批车获利最多?
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 .

(1)在图中画出△A1B1C1;
(2)点A1 , B1 , C1的坐标分别为、、;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )

A. 14cm B. 17cm C. 20cm D. 23cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)
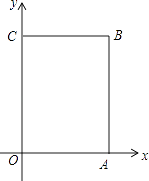
(1)写出B点的坐标();
(2)当点P移动了4秒时,在图中平面直角坐标系中描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间t.
相关试题

