【题目】已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)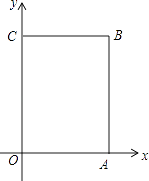
(1)写出B点的坐标();
(2)当点P移动了4秒时,在图中平面直角坐标系中描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间t.
参考答案:
【答案】
(1)4,6
(2)解:由每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动),
点P移动了4秒,得P点移动了8个单位,即OA+AP=8,
P点在AB上且距A点4个单位,
P(4,4)
(3)解:第一次距x轴5个单位时AP=5,即OA+AP=9=2t,
解得t= ![]() ,
,
第二次距x轴5个单位时,OP=5,即 OA+AB+BC+CP=4+6+4+6﹣5=2t,解得t= ![]() ,
,
综上所述:t= ![]() 秒,或t=
秒,或t= ![]() 秒时,点P到x轴的距离为5个单位长度.
秒时,点P到x轴的距离为5个单位长度.
【解析】解:(1)由矩形的性质,得
CB=OA=4,AB=OC=6,
B(4,6);
故答案为:4,6;
(1)根据矩形的对边相等,可得CB,AB的长,根据点的坐标表示方法,可得答案;(2)根据速度乘时间等于路程,可得OA+AP的长度,根据点的坐标表示方法,可得答案;(3)分类讨论:①OA+AP=9=2t,②OA+AB+BC+CP=4+6+4+6﹣5=2t,根据解方程,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;月均用水量x(t)
频数(户)
频率
0<x≤5
6
0.12
5<x≤10
0.24
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
4
25<x≤30
2
0.04
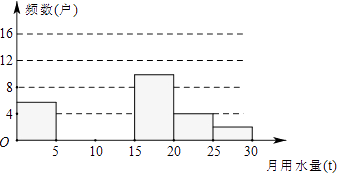
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个长方形的周长为10,其中长为a,那么该长方形的面积为( )
A.10a
B.5a﹣a2
C.5a
D.10a﹣a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线
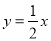 于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和
于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和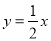 于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)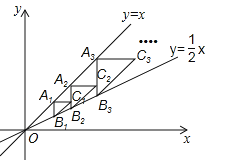
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的三边长分别为3,4,x,则x2为( )
A. 5 B. 25 C. 7 D. 7或25
相关试题

