搜索
【题目】如图，将△ABC沿射线BC方向平移3cm得到△DEF．若△ABC的周长为14cm，则四边形ABFD的周长为（ ）
A. 14cm B. 17cm C. 20cm D. 23cm
参考答案：
【答案】C
【解析】
先根据平移的性质得DF=AC，AD=CF=3cm，再由△ABC的周长为14cm得到AB+BC+AC=14cm，然后利用等线段代换可计算出AB+BC+CF+DF+AD=20（cm），于是得到四边形ABFD的周长为20cm．
∵△ABC沿BC方向平移3cm得到△DEF，
∴DF=AC，AD=CF=3cm，
∵△ABC的周长为14cm，即AB+BC+AC=14cm，
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=14+3+3=20（cm），
即四边形ABFD的周长为20cm．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．
（1）求证：△DEC≌△EDA；
（2）求DF的值；
（3）如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其顶点Q落在线段AE上，定点M、N落在线段AC上，当线段PE的长为何值时，矩形PQMN的面积最大？并求出其最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c（a≠0）的图象过点M（﹣2，
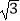），顶点坐标为N（﹣1， 
），且与x轴交于A、B两点，与y轴交于C点．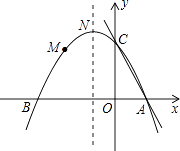
（1）求抛物线的解析式；
（2）点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标；
（3）在直线AC上是否存在一点Q，使△QBM的周长最小？若存在，求出Q点坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在△ABC中，∠C=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于M，BN⊥MN于N。
（1）求证：MN=AM+BN；
（2）若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】某同学在计算3（4+1）（42+1）时，把3写成（4﹣1）后，发现可以连续运用平方差公式计算：3（4+1）（42+1）＝（4﹣1）（4+1）（42+1）＝（42﹣1）（42+1）＝（42）2﹣12＝256﹣1＝255．请借鉴该同学的方法计算（2+1）（22+1）（24+1）（28+1）…（22048+1）＝______
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）请用两种不同的方法列代数式表示图1阴影部分的面积．
方法①：__________________________；
方法②：____________________________；
（2）根据（1）写出一个等式：__________________________.
（3）有许多代数恒等式可以用图形的面积来表示．如图2，它表示了（2m+n）(m+n)=2m2+3mn+n2.
试画出一个几何图形，使它的面积能表示（2m+n）(m+2n)=2m2+5mn+2n2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
相关试题
