【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.

参考答案:
【答案】(1)、y=﹣x2+8x﹣15;(2)、1;(3)、(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】试题分析:(1)、先依据配方法求得抛物线C1的顶点坐标,然后令y=0,求得点A、B的坐标,从而可判断出C1平移的方向和距离,于是得到抛物线C2的顶点坐标,从而得到C2的解析式;(2)、根据函数图象可知,当点D为C2的顶点时,△ABD的面积最大;(3)、设点E的坐标为(x,﹣x2+4x﹣3),则点F的坐标为(x,﹣x2+8x﹣15),然后可求得EF长度的解析式,最后根据EF=5,可列出关于x的方程,从而可求得x的值,于是的得到点E的坐标.
试题解析:(1)、∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,∴抛物线C1的顶点坐标为(2,1).
令y=0,得﹣(x﹣2)2+1=0,解得:x1=1,x2=3.∵C2经过B,∴C1向右平移了2个单位长度.
∵将抛物线向右平移两个单位时,抛物线C2的顶点坐标为(4,1),
∴C2的解析式为y2=﹣(x﹣4)2+1,即y=﹣x2+8x﹣15.
(2)、根据函数图象可知,当点D为C2的顶点时,纵坐标最大,即D(4,1)时,△ABD的面积最大
S△ABD=![]() AB|yD|=
AB|yD|=![]() ×2×1=1.
×2×1=1.
(3)、设点E的坐标为(x,﹣x2+4x﹣3),则点F的坐标为(x,﹣x2+8x﹣15).
EF=|(﹣x2+4x﹣3)﹣(﹣x2+8x﹣15)|=|﹣4x+12|.∵EF=5,∴﹣4x+12=5或﹣4x+12=﹣5.
解得:x=![]() 或x=
或x=![]() .
.
∴点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )时,EF=5.
)时,EF=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计显示,2013年底杭州市各类高中在校学生人数大约是11.4万人,将11.4万用科学记数法表示应为( )
A.11.4×102
B.1.14×103
C.1.14×104
D.1.14×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.
(1)设一本书的厚度为acm,则EF= cm(结果保留根号);
(2)若书的长度AB=20cm,求一本书的厚度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,b)在一次函数y=2x+1的图象上,则4a﹣2b﹣1=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
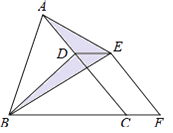
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是°.

相关试题

