Question

【题目】如图，已知△ABC的面积为24，点D在线段AC上，点F在线段BC的延长线上，且BF=4CF，四边形DCFE是平行四边形，则图中阴影部分的面积为（ ）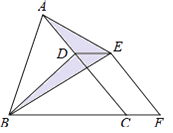

A.3
B.4
C.6
D.8

Answer 1

【答案】A
【解析】连接EC，过A作AM∥BC交FE的延长线于M，

∵四边形CDEF是平行四边形，
∴DE∥CF，EF∥CD，
∴AM∥DE∥CF，AC∥FM，
∴四边形ACFM是平行四边形，
∵△BDE边DE上的高和△CDE的边DE上的高相同，
∴△BDE的面积和△CDE的面积相等，
同理△ADE的面积和△AME的面积相等，
即阴影部分的面积等于平行四边形ACFM的面积的一半，是 × CF×hCF ，
∵△ABC的面积是24，BC=4CF
∴ BC×hBC= ×4CF×hCF=24，
∴CF×hCF=12，
∴阴影部分的面积是 × ×12=3，
故答案为：A．
连接EC，过A作AM∥BC交FE的延长线于M，根据已知易证四边形ACFM是平行四边形，根据同底等高的两个三角形的面积相等，得出△BDE的面积和△CDE的面积相等，△ADE的面积和△AME的面积相等，从而证得阴影部分的面积等于平行四边形ACFM的面积的一半，就可求出CF×hCF的值，即可得出答案。