搜索
【题目】东台教育局为帮助全市贫困师生举行“一日捐”活动，甲、乙两校教师各捐款30000元，已知“……”，设乙学校教师有x人，则可得方程
，根据此情景，题中用“……”表示的缺失的条件应补（ ）
A. 乙校教师比甲校教师人均多捐20元，且甲校教师的人数比乙校教师的人数多20%
B. 甲校教师比乙校教师人均多捐20元，且乙校教师的人数比甲校教师的人数多20%
C. 甲校教师比乙校教师人均多捐20元，且甲校教师的人数比乙校教师的人数多20%
D. 乙校教师比甲校教师人均多捐20元，且乙校教师的人数比甲校教师的人数多20%
参考答案：
【答案】A
【解析】设乙学校教师有x人，那么当甲校教师的人数比乙校教师的人数多20%时，甲校教师有（1+20%）x人．如果乙校教师比甲校教师人均多捐20元，那么可列出方程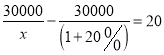
．
故选A．
-
科目： 来源： 题型：
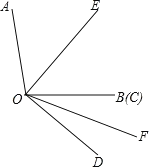
查看答案和解析>>【题目】已知∠AOB=100°，∠COD=40°，OE平分∠AOC，OF平分∠BOD.（本题中的角均为大于0°且小于等于180°的角）.
（1）如图1，当OB、OC重合时，求∠EOF的度数；
（2）当∠COD从图1所示位置绕点O顺时针旋转n°（0＜n＜90）时，∠AOE﹣∠BOF的值是否为定值？若是定值，求出∠AOE﹣∠BOF的值；若不是，请说明理由.
（3）当∠COD从图1所示位置绕点O顺时针旋转n°（0＜n＜180）时，满足∠AOD+∠EOF=6∠COD，则n=__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】运用加法的运算律计算(＋6
)＋(－18)＋(＋4
)＋(－6.8)＋18＋(－3.2)最适当的是( )A. [ (＋6
)＋ (＋4)＋18]+[ (－18)＋(－6.8)＋(－3.2)]B. [ (＋6
)＋ (-6.8)＋(＋4)]＋[(－18)＋18＋(－3.2)]C. [ (＋6
)＋ (-18)]+[ (＋4)＋(－6.8)]＋[18＋(－3.2)]D. [ (＋6
)＋ (＋4)]＋[(－18)＋18]＋[(－3.2)＋(－6.8)] -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰直角三角形
和
中，点
为它们的直角顶点,当
与
有重叠部分时：（1）①连接
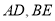，如图1，求证： 
；②连接
，如图2，求证： 
；（2）当
与
无重叠部分时：连接
,如图3，当
， 
时，计算四边形
面积的最大值，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中不一定成立的是（ ）
A. S△BEC=2S△CEF B. EF=CF
C. ∠DCF=
∠BCD D. ∠DFE=3∠AEF -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
(1)0.36＋(－7.4)＋0.3＋(－0.6)＋0.64；(2)3
＋(-2
)＋5
＋(-8
)；(3)(－103)＋(＋1
)＋(－97)＋(＋100)＋(－1
)；(4)(-2
)＋(－0.38)＋(-)＋(＋0.38)；(5)(－9
)＋15＋(－3)＋(－22.5)＋(－15
)；(6)[(+
)+(-3.5)+(-6)]＋[(＋2.5)＋(＋6)＋(+
)]． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，CD是边AB上的高，且
=
．
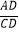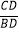（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．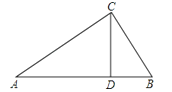
相关试题
