【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x 件,已知产销两种产品的有关信息 如下:
产品 | 每件售价/万元 | 每件成本/万元 | 年最大产销量/件 |
甲 | 6 | 3 | 200 |
乙 | 20 | 10 | 80 |
甲、乙两产品每年的其他费用与产销量的关系分别是: y1 kx b 和 y2 ax2 m ,它们的函数图象分别如图(1)和图(2)所示.


(1)求: y1 、 y2 的函数解析式;
(2)分别求出产销两种产品的最大利润;(利润=销售额-成本-其它费用)
(3)若通过技术改进,甲产品的每件成本降到 a 万元,乙产品的年最大产销量可以达到 110 件,其它都不变,为获得最大利润,该公式应该选择产销哪种产品?请说明理由.
参考答案:
【答案】,(1)![]() ,
,![]() ;(2)x=200时,
;(2)x=200时,![]() ,x=80时,
,x=80时,![]() ;(3)当
;(3)当![]() 时,选择两种产品一样,当
时,选择两种产品一样,当![]() 时,选择甲产品,当
时,选择甲产品,当![]() 时,选择乙产品,理由见解析.
时,选择乙产品,理由见解析.
【解析】
(1)用待定系数法求函数解析式;(2)先列出二次函数,根据二次根式的顶点确定函数的最值;(3))根据![]() ,
,
![]() ,根据函数的最值关系,分三种情况分析.
,根据函数的最值关系,分三种情况分析.
解:(1)依题意得:![]() ,所以
,所以 ![]() ,所以,
,所以, ![]() ;
;
由已知可得:![]() ,所以,
,所以, ![]() ,所以,
,所以, ![]() .
.
(2)![]() , (
, (![]() ),
),
2>0,![]() ,
,
∴x=200时,![]() .
.
![]() ,(
,(![]() ).
).
![]() ,
,![]() 时,
时,![]()
∴x=80时,![]() .
.
(3)![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,
∴x=200时,![]() ,
,
![]() ,
, ![]() ,
,
∴x=100时,![]() ,
,
①![]() ,解得
,解得![]() ,
,
当![]() 时,选择两种产品一样.
时,选择两种产品一样.
②![]() 解得
解得 ![]() ,
,
当![]() 时,选择甲产品.
时,选择甲产品.
③![]() ,解得
,解得 ![]()
当![]() 时,选择乙产品.
时,选择乙产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黑板上写有1,2,3,…,2019,2020这2020个自然数,对它们进行操作,每次操作规则如下:擦掉写在黑板上的三个数后,再添写上所擦掉三个数之和的个位数字,例如:擦掉5,13和2010后,添加上8;若再擦掉8,8,38,添上4,等等.如果经过1004次操作后,发现黑板上剩下两个数,一个是29,求另一个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在 Rt△ABC 中,∠C=Rt∠,AC=2BC,AB=5,D、E 分别在 AB、AC 上,且 AE
 ,DE∥BC.
,DE∥BC.(1)如图(1),将△ADE 沿射线 DA 方向平移,得到△ A1 D1 E1 ,当 AD1 多大时,四边形 AA1 E1 E 为菱形;
(2)如图(2),将△ADE 绕 A 点顺时针旋转 度( 00 1800 )得到△AD2E2
①连结 CE2 , BD2 ,求:
 的值;
的值;②连结 CE2 , BE2 若△ ACE2 是直角三角形,求:△ ABE 2 的面积.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠BAC=∠BFC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5的网格中,最小正方形的边长为1,A,B,C,D均为格点(最小正方形的顶点).
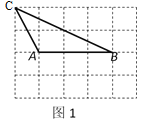
(1)如图1,画出所有以AB为一边且与△ABC全等的格点三角形.
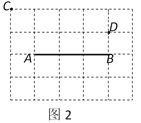
(2)如图2,在线段AB上画出一点P,使CP+PD最小,其最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中, ∠C=90°,边AB的垂直平分线交AB、AC分别于点D,点E,连结BE.

(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的面积.
相关试题

