搜索
【题目】如图，△ABC中， ∠C=90°，边AB的垂直平分线交AB、AC分别于点D，点E，连结BE．
（1）若∠A=40°，求∠CBE的度数．
（2）若AB=10，BC=6，求△BCE的面积．
参考答案：
【答案】（1）10°；（2）
【解析】
（1）由AB的垂直平分线DE交AC于点E，可得AE=BE，继而求得∠ABE的度数，然后由Rt△ABC中，∠C=90°，求得∠ABC的度数，继而求得答案；
（2）根据勾股定理得到AC=8，根据线段的垂直平分线的性质得到AE=BE，即可得到结论．
（1）∵∠C=
，∠A=40°，
∴∠CBA=
，
∵DE是AB的垂直平分线
∴BE=AE，
∴∠EBA=∠A=40°，
∴∠CBE=∠CBA—∠EBA =10°；
（2）∵ AB=10，BC=6，
∴AC=
=8，
设CE=
，则AE=BE=
∴
，
解得：
，
∴△BCE的面积为.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销 x 件，已知产销两种产品的有关信息 如下：
产品
每件售价/万元
每件成本/万元
年最大产销量/件
甲
6
3
200
乙
20
10
80
甲、乙两产品每年的其他费用与产销量的关系分别是： y1 kx b 和 y2 ax2 m ，它们的函数图象分别如图（1）和图（2）所示.
（1）求： y1 、 y2 的函数解析式；
（2）分别求出产销两种产品的最大利润；（利润=销售额-成本-其它费用）
（3）若通过技术改进，甲产品的每件成本降到 a 万元，乙产品的年最大产销量可以达到 110 件，其它都不变，为获得最大利润，该公式应该选择产销哪种产品？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB．添加一个条件，不能使四边形DBCE成为矩形的是（ ）
（A）AB=BE （B）BE⊥DC （C）∠ADB=90° （D）CE⊥DE
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在4×5的网格中，最小正方形的边长为1，A，B，C，D均为格点（最小正方形的顶点）．
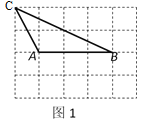
（1）如图1，画出所有以AB为一边且与△ABC全等的格点三角形．
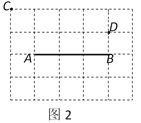
（2）如图2，在线段AB上画出一点P，使CP+PD最小，其最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，然后解决问题：和、差、倍、分等问题中有着广泛的应用，
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．
（1）如图1，在△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是 ；
（2）问题解决：
如图2，在四边形ABCD中，AB=AD，∠ABC+∠ADC=180°，E、F分别是边BC，边CD上的两点，且∠EAF=
∠BAD，求证：BE+DF=EF．（3）问题拓展：
如图3，在△ABC中，∠ACB=90°，∠CAB=60°，点D是△ABC外角平分线上一点，DE⊥AC交CA延长线于点E，F是AC上一点，且DF=DB．求证：AC-AE=
AF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD，CG，有下列结论：①∠BGD=120° ；②BG+DG=CG；③△BDF≌△CGB；④
．其中正确的结论有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）
A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA
相关试题
