【题目】如图1,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
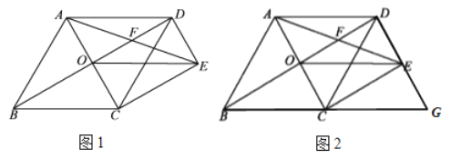
(1)求证:![]() ;
;
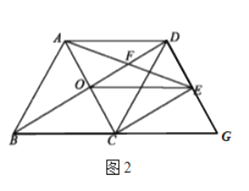
(2)如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形
,不添加任何辅助线的情况下,直接写出图中所有的平行四边形.(除四边形![]() 和四边形
和四边形![]() 外)
外)
参考答案:
【答案】(1)证明见解析,(2)图中的平行四边形有:平行四边形![]() ,平行四边形
,平行四边形![]() ,平行四边形
,平行四边形![]() ,平行四边形
,平行四边形![]() .
.
【解析】
(1)由菱形![]() 的性质得到:
的性质得到:![]() ,结合已知条件证明四边形
,结合已知条件证明四边形![]() 为矩形,可得答案.
为矩形,可得答案.
(2)利用菱形的性质,结合(1)问的结论,得到四边形![]() 为平行四边形,其它的平行四边形可依次得到.
为平行四边形,其它的平行四边形可依次得到.
证明:![]() (1)菱形
(1)菱形![]() ,
,
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]() 四边形
四边形![]() 为矩形.
为矩形.
![]()
(2)图中的平行四边形有:平行四边形![]() ,平行四边形
,平行四边形![]() ,平行四边形
,平行四边形![]() ,平行四边形
,平行四边形![]() ,
,
理由如下:![]() 菱形
菱形![]() ,
,
![]()
![]()
![]() 四边形
四边形![]() 为矩形.
为矩形.
![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
![]() 四边形
四边形![]() ,四边形
,四边形![]() ,四边形
,四边形![]() 都是平行四边形,
都是平行四边形,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.

(1)求证:△BOE≌△DOF;
(2)若
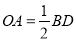 ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,延长平行四边形
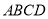 的边
的边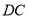 到点
到点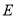 ,使
,使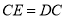 ,连接
,连接 交
交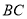 于点
于点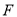 .
.(1)求证:
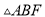 ≌
≌ .
.(2)连接
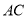 、
、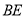 ,若
,若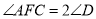 ,求证四边形
,求证四边形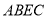 是矩形.
是矩形.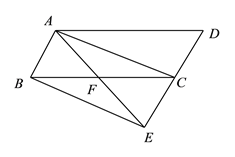
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.

证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区进行环境改造,计划用地面砖铺设楼前矩形广场的地面
 ,已知矩形广场地面的长为100米,宽为80米,图案设计如图所示:广场的四角为边长相同的小正方形,阴影分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
,已知矩形广场地面的长为100米,宽为80米,图案设计如图所示:广场的四角为边长相同的小正方形,阴影分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
(1)要使铺白色地面砖的面积为5200平方米,并且四个角的小正方形面积的和不超过500平方米,那么这个矩形广场的四个角的小正方形的边长应为多少米?
(2)在(1)的条件下,为了增加广场的绿化同时节省开支,现将广场四角的白色正方形地面砖的
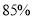 中的一部分改为种植绿色景观,另一部分铺设绿色地面砖.经过市场调查了解到种植绿色景观每平方米的费用为30元,白色地面砖每平方米的费用为20元,绿色地面砖每平方米的费用为10元.若广场四角的总费用不超过9400元,则最多可以将多少面积的白色地面砖改为种植绿色景观?
中的一部分改为种植绿色景观,另一部分铺设绿色地面砖.经过市场调查了解到种植绿色景观每平方米的费用为30元,白色地面砖每平方米的费用为20元,绿色地面砖每平方米的费用为10元.若广场四角的总费用不超过9400元,则最多可以将多少面积的白色地面砖改为种植绿色景观? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,点
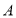 坐标
坐标 ,点
,点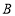 坐标
坐标 ,连接
,连接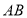 ,
,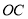 平分
平分 交
交 于点
于点 .
.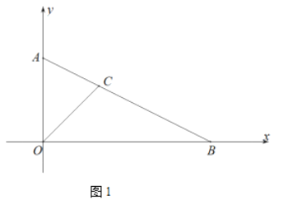
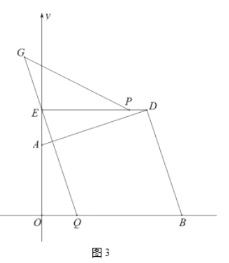
(1)如图1,求
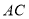 的长;
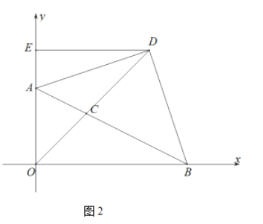
的长;(2)如图2,
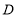 是
是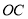 延长线上一点,连接
延长线上一点,连接 ,
,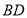 ,且
,且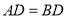 ,过点
,过点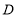 作
作 轴于点
轴于点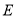 ,若点
,若点 是线段
是线段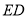 上一点,点
上一点,点 的横坐标为
的横坐标为 ,连接
,连接 ,设
,设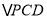 的面积为
的面积为 ,求
,求 与
与 的关系;
的关系;(3)在(2)的条件下,如图3,线段
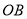 上存在一点
上存在一点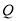 ,使得
,使得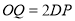 ,点
,点 在
在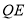 的延长线上,且
的延长线上,且 ,连接
,连接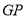 ,若
,若 ,求点
,求点 的坐标及
的坐标及 值?
值? -
科目: 来源: 题型:
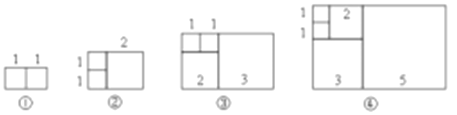
查看答案和解析>>【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的长方形,依次记作长方形①、长方形②、长方形③、长方形④,那么按此规律,长方形⑥的周长为_____.
相关试题

