【题目】在4张完全相同的卡片正面分别写上数字1,2,3,3,现将它们的背面朝上洗均匀.
(1)随机抽出一张卡片,求抽到数字“3”的概率;
(2)若随机抽出一张卡片记下数字后放回并洗均匀,再随机抽出一张卡片,求两次都是抽到数字“3”的概率;(要求画树状图或列表求解)
(3)如果再增加若干张写有数字“3”的同样卡片,洗均匀后,使得随机抽出一张卡片是数字“3”的概率为 ![]() ,问增加了多少张卡片?
,问增加了多少张卡片?
参考答案:
【答案】
(1)解:∵有4张完全相同的卡片正面分别写上数字1,2,3,3,抽到数字“3”的有2种情况,
∴随机抽出一张卡片,抽到数字“3”的概率为: ![]() =
= ![]()
(2)解:列表得:
第二张 第一张 | 1 | 2 | 3 | 3 |
1 | (1,1) | (1,2) | (1,3) | (1,3) |
2 | (2,1) | (2,2) | (2,3) | (2,3) |
3 | (3,1) | (3,2) | (3,3) | (3,3) |
3 | (3,1) | (3,2) | (3,3) | (3,3) |
∵共有16种等可能的结果,两次都是抽到数字“3”的有4种情况,
∴P(两次都是抽到数字“3”)= ![]() =
= ![]()
(3)解:设增加了x张卡片,则有:
![]() =
= ![]() ,
,
解得:x=4,
∴增加了4张卡片
【解析】(1)由有4张完全相同的卡片正面分别写上数字1,2,3,3,抽到数字“3”的有2种情况,利用概率公式求解即可求得答案;(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与两次都是抽到数字“3”的情况,再利用概率公式求解即可求得答案;(3)首先设增加了x张卡片,即可得方程: ![]() =
= ![]() ,解此方程即可求得答案.
,解此方程即可求得答案.
【考点精析】通过灵活运用列表法与树状图法和概率公式,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2
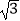 ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,线段AB的两个端点的坐标分别为A(﹣3,0),B(0,4).

(1)画出线段AB先向右平移3个单位,再向下平移4个单位后得到的线段CD,并写出A的对应点D的坐标,B的对应点C的坐标;
(2)连接AD、BC,判断所得图形的形状.(直接回答,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整).

(1)此次共调查了多少位学生?
(2)将表格填充完整;步行
骑自行车
坐公共汽车
其他
50
(3)将条形统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证:

(1)△ABF≌△DEA;
(2)DF是∠EDC的平分线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE.

(1)求证:FC为⊙O的切线;
(2)若△ADC是边长为a的等边三角形,求AB的长.(用含a的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1 , y1),Q(x2 , y2)为端点的线段的中点坐标为( ,
,  ).如图,在平面直角坐标系xOy中,双曲线y=
).如图,在平面直角坐标系xOy中,双曲线y=  (x<0)和y=
(x<0)和y=  (x>0)的图象关于y轴对称,直线y=
(x>0)的图象关于y轴对称,直线y=  +
+  与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
相关试题

