Question

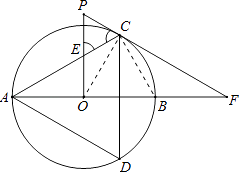
【题目】如图，以AB为直径的⊙O是△ADC的外接圆，过点O作PO⊥AB，交AC于点E，PC的延长线交AB的延长线于点F，∠PEC=∠PCE．
（1）求证：FC为⊙O的切线；
（2）若△ADC是边长为a的等边三角形，求AB的长．（用含a的代数式表示）

Answer 1

【答案】
（1）证明：连接OC．

∵OA=OC（⊙O的半径），

∴∠EAO=∠ECO（等边对等角）．

∵PO⊥AB，∴∠EAO+∠AEO=90°（直角三角形中的两个锐角互余）．

∵∠PEC=∠PCE（已知），∠PEC=∠AEO（对顶角相等）

∴∠AEO=∠PCE（等量代换），

∴∠PCO=∠ECO+∠PCE=∠EAO+∠AEO=90°．即OC⊥FC，

∵点C在⊙O上，

∴FC为⊙O的切线

（2）解：连接BC．

∵AB是⊙O的直径，∴∠ACB=90°．

∵△ADC是边长为a的等边三角形，

∴∠ABC=∠D=60°，AC=a．

在Rt△ACB中，∵sin∠ABC=

∴AB= = a．

【解析】（1）连接OC．欲证FC为⊙O的切线，只需证明OC⊥FC即可；（2）连接BC．由等边三角形的性质、“同弧所对的圆周角相等”推知∠ABC=∠ADC=60°；然后在直角△ABC中利用正弦三角函数的定义来求AB线段的长度．
【考点精析】掌握等边三角形的性质和切线的判定定理是解答本题的根本，需要知道等边三角形的三个角都相等并且每个角都是60°；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．