【题目】在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E、F分别在边
,点E、F分别在边![]() 、
、![]() 上,
上,![]() ,点P与
,点P与![]() 在直线
在直线![]() 的两侧,
的两侧,![]() ,
,![]() ,射线
,射线![]() 、
、![]() 与边
与边![]() 分别相交于点M、N,设
分别相交于点M、N,设![]() ,
,![]() .
.
(1)求边![]() 的长;
的长;
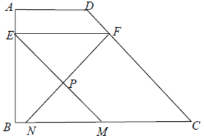
(2)如图,当点P在梯形![]() 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;
(3)如果![]() 的长为2,求梯形
的长为2,求梯形![]() 的面积.
的面积.
参考答案:
【答案】(1)6;(2)y=-3x+10(1≤x<![]() );(2)
);(2)![]() 或32
或32
【解析】
(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;
(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;
(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.
(1)如下图,过点D作BC的垂线,交BC于点H

∵∠C=45°,DH⊥BC
∴△DHC是等腰直角三角形
∵四边形ABCD是梯形,∠B=90°
∴四边形ABHD是矩形,∴DH=AB=8
∴HC=8
∴BH=BC-HC=6
∴AD=6
(2)如下图,过点P作EF的垂线,交EF于点Q,反向延长交BC于点R,DH与EF交于点G

∵EF∥AD,∴EF∥BC
∴∠EFP=∠C=45°
∵EP⊥PF
∴△EPF是等腰直角三角形
同理,还可得△NPM和△DGF也是等腰直角三角形
∵AE=x
∴DG=x=GF,∴EF=AD+GF=6+x
∵PQ⊥EF,∴PQ=QE=QF
∴PQ=![]()
同理,PR=![]()
∵AB=8,∴EB=8-x
∵EB=QR
∴8-x=![]()
化简得:y=-3x+10
∵y>0,∴x<![]()
当点N与点B重合时,x可取得最小值
则BC=NM+MC=NM+EF=-3x+10+![]() ,解得x=1
,解得x=1
∴1≤x<![]()
(3)情况一:点P在梯形ABCD内,即(2)中的图形
∵MN=2,即y=2,代入(2)中的关系式可得:x=![]() =AE
=AE
∴![]()
情况二:点P在梯形ABCD外,图形如下:

与(2)相同,可得y=3x-10
则当y=2时,x=4,即AE=4
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有 (多选、错选不得分).
①∠A+∠B=90°
②AB2=AC2+BC2
③

④CD2=ADBD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有关于
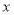 ,
,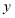 的方程
的方程 .
.(1)当
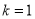 和
和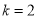 时,所得方程组成的方程组是
时,所得方程组成的方程组是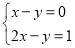 ,它的解是______;
,它的解是______;(2)当
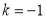 和
和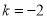 时,所得方程组成的方程组是______它的解是______;
时,所得方程组成的方程组是______它的解是______;(3)猜想:无论
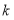 取何值,关于
取何值,关于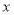 ,
,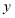 的方程
的方程 一定有一个解是______.
一定有一个解是______.(4)猜想:无论
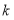 取何值,关于
取何值,关于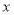 ,
,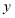 的方程
的方程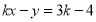 一定有一个解是______.
一定有一个解是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点B、C为线段AD上的两点,AB=
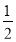 BC=
BC= CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=3,BC=4,AB=5,D、E分别是边AB、边BC上的点,把△ABC沿着直线DE对折,顶点B的对应点是点
 .
.(1)如图1,如果点
 和顶点A重合,求CE的长;
和顶点A重合,求CE的长;(2)如图2,如果点
 落在AC的中点,求CE的长.
落在AC的中点,求CE的长.
-
科目: 来源: 题型:
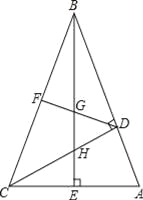
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
相关试题

