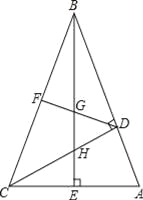
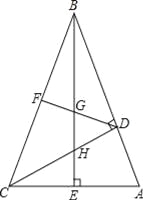
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
参考答案:
【答案】解:(1)线段BH与AC相等。证明如下:
∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°,
∴∠BCD=45°=∠ABC,∠A+∠DCA=90°,∠A+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA,
在△DBH和△DCA中,∵∠DBH=∠DCA,BD=CD,∠BDH=∠CDA,
∴△DBH≌△DCA(ASA)。∴BH=AC。
(2)证明:连接CG,
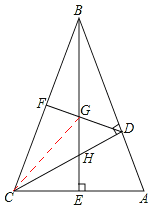
∵F为BC的中点,DB=DC,∴DF垂直平分BC。∴BG=CG。
∵∠ABE=∠CBE,BE⊥AC,∴∠AEB=∠CEB。
在△ABE和△CBE中,
∵∠AEB=∠CEB,BE=BE,∠CBE=∠ABE,
∴△ABE≌△CBE(ASA)。∴EC=EA。
在Rt△CGE中,由勾股定理得:CG2﹣GE2=EC2。
∴BG2﹣GE2=EA2。
【解析】试题分析:(1)、根据三角形的内角和定理求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△DBH≌△DCA即可;(2)、根据DB=DC和F为BC中点,得出DF垂直平分BC,推出BG=CG,根据BE⊥AC和∠ABE=∠CBE得出AE=CE,在Rt△CGE中,由勾股定理即可推出答案.
试题解析:(1)、BH=AC,理由如下: ∵CD⊥AB,BE⊥AC, ∴∠BDH=∠BEC=∠CDA=90°, ∵∠ABC=45°,
∴∠BCD=180°﹣90°﹣45°=45°=∠ABC ∴DB=DC, ∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°, ∴∠HBD=∠ACD, ∵在△DBH和△DCA中
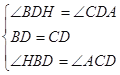 , ∴△DBH≌△DCA(ASA), ∴BH=AC.
, ∴△DBH≌△DCA(ASA), ∴BH=AC.
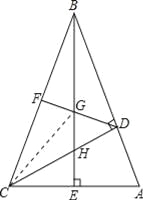
(2)、连接CG, 由(1)知,DB=CD, ∵F为BC的中点, ∴DF垂直平分BC, ∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC, ∴EC=EA, 在Rt△CGE中,由勾股定理得:CG2﹣GE2=CE2,
∵CE=AE,BG=CG, ∴BG2﹣GE2=EA2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形
 中,
中,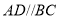 ,
,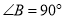 ,
,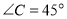 ,
,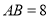 ,
,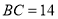 ,点E、F分别在边
,点E、F分别在边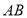 、
、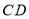 上,
上,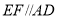 ,点P与
,点P与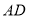 在直线
在直线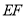 的两侧,
的两侧,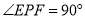 ,
,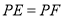 ,射线
,射线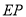 、
、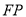 与边
与边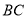 分别相交于点M、N,设
分别相交于点M、N,设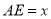 ,
,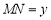 .
.
(1)求边
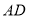 的长;
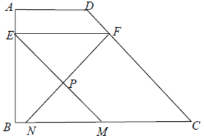
的长;(2)如图,当点P在梯形
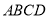 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;(3)如果
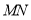 的长为2,求梯形
的长为2,求梯形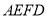 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点B、C为线段AD上的两点,AB=
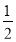 BC=
BC= CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=3,BC=4,AB=5,D、E分别是边AB、边BC上的点,把△ABC沿着直线DE对折,顶点B的对应点是点
 .
.(1)如图1,如果点
 和顶点A重合,求CE的长;
和顶点A重合,求CE的长;(2)如图2,如果点
 落在AC的中点,求CE的长.
落在AC的中点,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )

A. 2条 B. 4条 C. 5条 D. 6条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与反比例函数
 的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若
的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若 <u<2,则v的取值范围是__________.
<u<2,则v的取值范围是__________.
相关试题

