【题目】如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有 (多选、错选不得分).
①∠A+∠B=90°
②AB2=AC2+BC2
③![]()
④CD2=ADBD.

参考答案:
【答案】①②④.
【解析】试题解析:①∵三角形内角和是180°,由①知∠A+∠B=90°,
∴∠ACB=180°-(∠A+∠B)=180°-90°=90°,
∴△ABC是直角三角形.故选项①正确.
②AB,AC,BC分别为△ABC三个边,由勾股定理的逆定理可知,②正确.
③题目所给的比例线段不是△ACB和△CDB的对应边,且夹角不相等,无法证明△ACB与△CDB相似,也就不能得到∠ACB是直角,故③错误;
④若△ABC是直角三角形,已知CD⊥AB,
又∵CD2=ADBD,(即 ![]() )
)
∴△ACD∽△CBD
∴∠ACD=∠B
∴∠ACB=∠ACD+∠DCB=∠B+∠DCB=90°
△ABC是直角三角形
∴故选项④正确;
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,如图,在平行四边形
 中,
中,  ,
,  ,
,  ,点
,点 为
为 边上任意一点,连接
边上任意一点,连接 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 得到线段
得到线段 .
.(
 )当
)当 时,求
时,求 的大小.
的大小.(
 )当
)当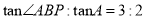 时,求点
时,求点 与点
与点 间的距离(结果保留根号).
间的距离(结果保留根号).(
 )若点
)若点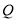 恰好落在平行四边形
恰好落在平行四边形 的边所在的条直线上,直接写出
的边所在的条直线上,直接写出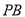 旋转到
旋转到 所扫过的面积(结果保留
所扫过的面积(结果保留 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把
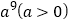 按下列要求进行操作:若指数为奇数则乘以
按下列要求进行操作:若指数为奇数则乘以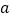 ,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时
,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时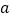 的指数为4?第10次操作时
的指数为4?第10次操作时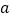 的指数是多少?你有什么发现?
的指数是多少?你有什么发现? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=2x+4的图象与x、y轴分别相交于点A、B,四边形ABCD是正方形.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有关于
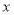 ,
,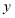 的方程
的方程 .
.(1)当
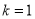 和
和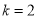 时,所得方程组成的方程组是
时,所得方程组成的方程组是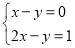 ,它的解是______;
,它的解是______;(2)当
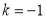 和
和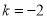 时,所得方程组成的方程组是______它的解是______;
时,所得方程组成的方程组是______它的解是______;(3)猜想:无论
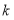 取何值,关于
取何值,关于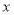 ,
,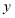 的方程
的方程 一定有一个解是______.
一定有一个解是______.(4)猜想:无论
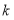 取何值,关于
取何值,关于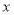 ,
,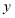 的方程
的方程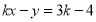 一定有一个解是______.
一定有一个解是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
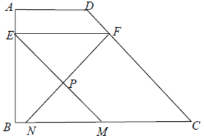
查看答案和解析>>【题目】在梯形
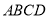 中,
中,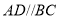 ,
,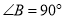 ,
,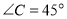 ,
,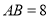 ,
,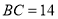 ,点E、F分别在边
,点E、F分别在边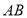 、
、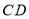 上,
上,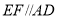 ,点P与
,点P与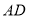 在直线
在直线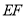 的两侧,
的两侧,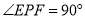 ,
,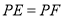 ,射线
,射线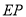 、
、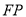 与边
与边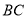 分别相交于点M、N,设
分别相交于点M、N,设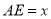 ,
,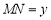 .
.
(1)求边
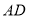 的长;
的长;(2)如图,当点P在梯形
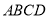 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;(3)如果
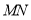 的长为2,求梯形
的长为2,求梯形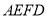 的面积.
的面积.
相关试题

