【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
参考答案:
【答案】D
【解析】分析:A、把m=-3代入[2m,1-m,-1-m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
B、令函数值为0,求得与x轴交点坐标,利用两点间距离公式解决问题;
C、首先求得对称轴,利用二次函数的性质解答即可;
D、根据特征数的特点,直接得出x的值,进一步验证即可解答.
详解:
因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m];
A、当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣![]() )2+
)2+![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() );此结论正确;
);此结论正确;
B、当m>0时,令y=0,有2mx2+(1﹣m)x+(﹣1﹣m)=0,解得:x1=1,x2=﹣![]() ﹣
﹣![]() ,
,
|x2﹣x1|=![]() +
+![]() >
>![]() ,所以当m>0时,函数图象截x轴所得的线段长度大于
,所以当m>0时,函数图象截x轴所得的线段长度大于![]() ,此结论正确;
,此结论正确;
C、当x=1时,y=2mx2+(1﹣m)x+(﹣1﹣m)=2m+(1﹣m)+(﹣1﹣m)=0 即对任意m,函数图象都经过点(1,0)那么同样的:当m=0时,函数图象都经过同一个点(1,0),当m≠0时,函数图象经过同一个点(1,0),故当m≠0时,函数图象经过x轴上一个定点此结论正确.
D、当m<0时,y=2mx2+(1﹣m)x+(﹣1﹣m) 是一个开口向下的抛物线,其对称轴是:直线x=![]() ,在对称轴的右边y随x的增大而减小.因为当m<0时,
,在对称轴的右边y随x的增大而减小.因为当m<0时,![]() ,即对称轴在x=
,即对称轴在x=![]() 右边,因此函数在x=
右边,因此函数在x=![]() 右边先递增到对称轴位置,再递减,此结论错误;
右边先递增到对称轴位置,再递减,此结论错误;
根据上面的分析,①②③都是正确的,④是错误的.
故选:D.
-
科目: 来源: 题型:
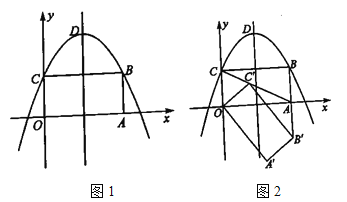
查看答案和解析>>【题目】如图1,以矩形
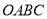 的顶点
的顶点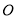 为原点,
为原点,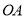 所在直线为
所在直线为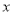 轴,
轴, 所在直线为
所在直线为 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点 的抛物线
的抛物线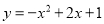 经过点
经过点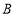 ,点
,点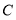 .
.
(1)写出抛物线的对称轴及点
 的坐标,
的坐标,(2)将矩形
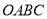 绕点
绕点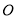 顺时针旋转
顺时针旋转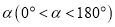 得到矩形
得到矩形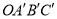 .
.①当点
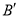 恰好落在
恰好落在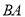 的延长线上时,如图2,求点
的延长线上时,如图2,求点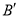 的坐标.
的坐标.②在旋转过程中,直线
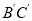 与直线
与直线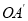 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点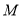 ,点
,点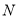 .若
.若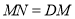 ,求点
,求点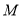 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(n,-n)在第二象限,过点M的直线y=kx+b(k>1)分别交x轴、y轴于点A、B,过点M作MN⊥x轴于点N,点P为线段AN上任意一点,则点P的横坐标可以是( )
A. (1+
 )nB. (1+
)nB. (1+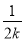 )nC. (1+k)nD. (1-k)n
)nC. (1+k)nD. (1-k)n -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(x1,y1),(x2,y2),(x3,y3)都在函数y=-2x+7的图象上,若数据x1,x2,x3的方差为5,则另一组数据y1,y2,y3的方差为_________.
-
科目: 来源: 题型:
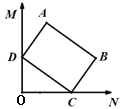
查看答案和解析>>【题目】如图,∠MON=90°,矩形ABCD的顶点C、D分别在边ON,OM上滑动,AB=9,BC=6,在滑动过程中,点A到点O的最大距离为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
相关试题

