【题目】如图1,以矩形![]() 的顶点
的顶点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
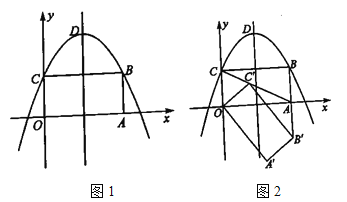
(1)写出抛物线的对称轴及点![]() 的坐标,
的坐标,
(2)将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到矩形
得到矩形![]() .
.
①当点![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求点
的延长线上时,如图2,求点![]() 的坐标.
的坐标.
②在旋转过程中,直线![]() 与直线
与直线![]() 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点![]() ,点
,点![]() .若
.若![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)对称轴:直线![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)首先根据矩形的性质以及A、C点的坐标确定点B的坐标,再利用待定系数法确定该抛物线的解析式.
(2) ①连结![]() 证明
证明![]() 即可解答
即可解答
②用全等或面积法证得![]() ,再分情况解得即可
,再分情况解得即可
解:(1)将y=0代入![]() 得C点的坐标为(0,1)则OC为1,则AB=1及B点的坐标为(2,1),再代入即可得对称轴:直线
得C点的坐标为(0,1)则OC为1,则AB=1及B点的坐标为(2,1),再代入即可得对称轴:直线![]()
(2)①连结![]() ,易知
,易知![]() ,
,
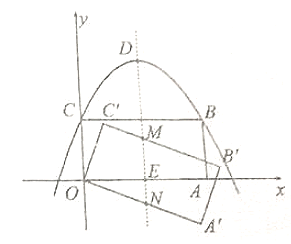
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
②可用全等或面积法证得![]() .(两张等宽纸条重叠部分为菱形)
.(两张等宽纸条重叠部分为菱形)
情况1:![]() ,如图.
,如图.
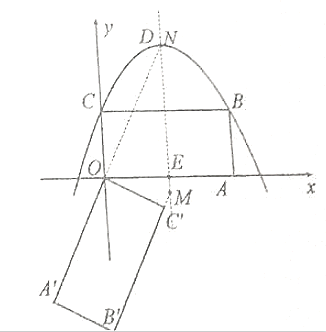
![]() 设
设![]() ,
,![]() ,
,
在![]() 中,
中,
![]()
![]() (舍去),
(舍去),![]()
![]()
情况2:![]() ,如图.
,如图. ![]()
此时点![]() 与点
与点![]() 重合,
重合,![]()
![]()
综上所述:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数
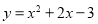 的图象如图所示,点
的图象如图所示,点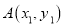 ,
,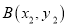 是该二次函数图象上的两点,其中
是该二次函数图象上的两点,其中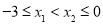 ,则下列结论正确的是( )
,则下列结论正确的是( )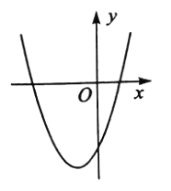
A.
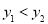 B.
B. 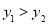 C. 函数
C. 函数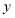 的最小值是
的最小值是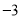 D. 函数
D. 函数 的最小值是
的最小值是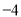
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点。设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为( )
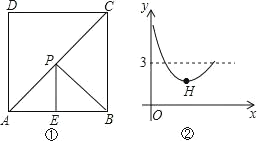
A. (1,2)B. (
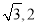 )C.
)C. 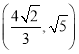 D.
D. 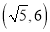
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(n,-n)在第二象限,过点M的直线y=kx+b(k>1)分别交x轴、y轴于点A、B,过点M作MN⊥x轴于点N,点P为线段AN上任意一点,则点P的横坐标可以是( )
A. (1+
 )nB. (1+
)nB. (1+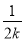 )nC. (1+k)nD. (1-k)n
)nC. (1+k)nD. (1-k)n -
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
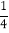 时,y随x的增大而减小
时,y随x的增大而减小
相关试题

