【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
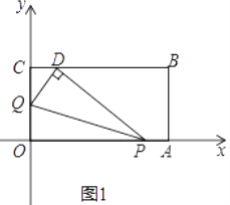
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
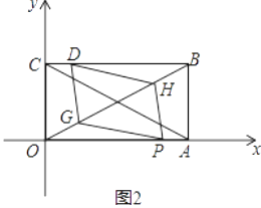
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形.
参考答案:
【答案】(1)B(6,3),OQ=![]() +t, OP= 6﹣t;(2)D(1,3);(3)证明见解析.
+t, OP= 6﹣t;(2)D(1,3);(3)证明见解析.
【解析】
试题(1)根据矩形的性质求出点B的坐标,根据动点问题求出OP和OQ的长度;(2)根据折叠图形的性质求出OQ和DQ的长度,然后根据勾股定理求出CD的长度,得到点D的坐标;(3)根据一组对边平行且相等的四边形为平行四边形进行判定.
试题解析:(1)B(6,3);OP="OA-AP=6-t," OQ=![]() +t.
+t.
(2)当t=1时,OP=5,OQ=![]() ,则CQ=3-
,则CQ=3-![]() =
=![]() ,
,
由折叠可知:△OPQ≌△DPQ,
∴OQ=DQ=![]()
由勾股定理,得:CD=1
∴D(1,3)
(3)∵四边形OABC是矩形,
∴OA=BC,
又∵CD=AP=1,
∴BC-CD=OA-AP,即BD=OP,
∵OM=MB,G为OM中点,H为BM中点 ,
∴OG="BH,"
∵OA∥BC
∴∠1=∠2
在△POG和△DBH中,OG=BH,∠1=∠2,OP=DB
∴△POG≌△DBH
∴∠OGP=∠BHD,PG=DH
∴∠MGP=∠DHM
∴PG∥DH
又∵PG=DH
∴四边形DGPH是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在
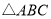 中,
中,  ,
,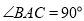 ,点
,点 、
、 为
为  边上两点, 将
边上两点, 将 、
、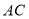 分别沿
分别沿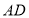 、
、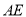 折叠,
折叠,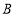 、
、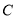 两点重合于点
两点重合于点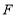 ,若
,若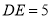 ,则
,则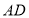 的长为__________.
的长为__________.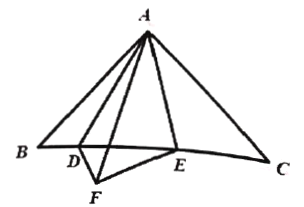
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形(非正方形)四个内角的平分线围成的四边形是__________形.(埴特殊四边形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
 为正方形,
为正方形, ,点
,点 为对角线
为对角线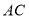 上一动点,连接
上一动点,连接 ,过点
,过点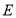 作
作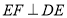 .交
.交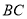 于点
于点 ,以
,以 、
、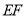 为邻边作矩形
为邻边作矩形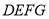 ,连接
,连接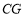 .
.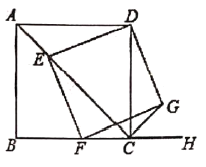
(1)求证:矩形
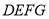 是正方形;
是正方形;(2)探究:
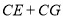 的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
的值是否为定值?若是,请求出这个定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)找规律:1,2,4,8……,则第n个数为________.
(2)求和
 ,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设:
,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设: ①
①两边乘以2得:
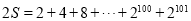 ②
②②-①得:
 ,所以:
,所以:
类比做一做,求
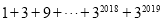 的值.
的值.(3)仿照(2)的做法求
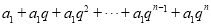 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生
 已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________. -
科目: 来源: 题型:
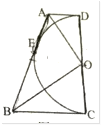
查看答案和解析>>【题目】如图,已知半圆
 与四边形
与四边形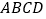 的边
的边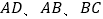 都相切,切点分别为
都相切,切点分别为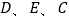 ,半径
,半径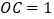 ,则
,则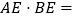 ___________.
___________.
相关试题

