搜索
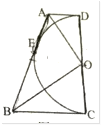
【题目】如图，已知半圆
与四边形
的边
都相切，切点分别为
，半径
，则
___________.
参考答案：
【答案】1
【解析】
连接 OE，由切线长定理可得∠AOE=
∠DOE，∠BOE=∠EOC，再根据∠DOE+∠EOC=180°，可得∠AOB=90°，继而可证△AEO∽△OEB，根据相似三角形对应边成比例即可得.
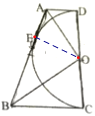
如图，连接 OE，
∵AD、AB与半圆 O 相切，
∴ OE⊥AB，OA平分∠DOE，
∴∠AOE=∠DOE，
同理∠BOE=∠EOC，
∵∠DOE+∠EOC=180°，
∴∠AOE+∠BOE=90°，
即∠AOB=90°，
∴∠ABO+∠BAO=90°，∵∠BAO+∠AOE=90°，
∴∠ABO=∠AOE，
∵∠OEA=∠BEO=90°，
∴△AEO∽△OEB，
∴AE：OE=OE：BE，
∴AEBE=OE=1，
故答案为：1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动
秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．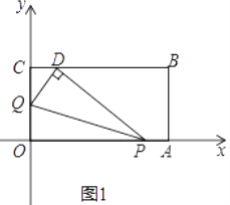
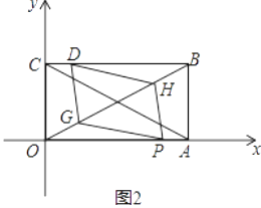
（1）求点B的坐标，并用含t的代数式表示OP，OQ；
（2）当t=1时，如图1，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；
（3）在（2）的条件下，矩形对角线AC，BO交于M，取OM中点G，BM中点H，求证：当t=1时四边形DGPH是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）找规律：1,2,4,8……，则第n个数为________．
（2）求和
，观察发现，从第2个加数起每一个加数都是前一个加数的2倍．于是可假设：
①两边乘以2得：
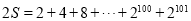②②-①得：
，所以：
类比做一做，求
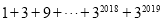的值．（3）仿照（2）的做法求
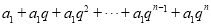的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】从2018年高中一年级学生开始，湖南省全面启动高考综合改革，学生学习完必修课程后，可以根据高校相关专业的选课要求和自身兴趣、志向、优势，从思想政治、历史、地理、物理、化学、生物6个科目中，自主选择3个科目参加等级考试.学生
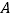已选物理，还想从思想政治、历史、地理3个文科科目中选1科，再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等，选化学、生物的可能性相等，则选修地理和生物的概率为___________. -
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．
（1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；
（2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A、B分别为数轴上的两点，A点对应的数为﹣20，B点对应的数为100．
（1）请写出与A，B两点距离相等的点M所对应的数 ．
（2）现有一只电子蚂蚁P从B点出发，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度向右运动，x秒后两只电子蚂蚁在数轴上的C点相遇，请列方程求出x，并指出点C表示的数．
（3）若当电子蚂蚁P从B点出发时，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度也向左运动，y秒后两只电子蚂蚁在数轴上的D点相遇，请列方程求出y并指出点D表示的数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：(
)﹣2﹣
+（
﹣4）0﹣
cos45°．【答案】1
【解析】试题分析：把原式的第一项根据负整数指数幂的意义化简，第二项根据算术平方根的定义求出9的算术平方根，第三项根据零指数公式化简，最后一项利用特殊角的三角函数值化简，合并后即可求出值.
试题解析：原式=4﹣3+1﹣
=2﹣1
=1．
【题型】解答题
【结束】
16【题目】《九章算术》“勾股”章有一题：“今有二人同所立，甲行率七，乙行率三．乙东行，甲南行十步而斜东北与乙会．问甲乙行各几何”．大意是说，已知甲、乙二人同时从同一地
点出发，甲的速度为7，乙的速度为3．乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇．那么相遇时，甲、乙各走了多远？
相关试题
