【题目】矩形(非正方形)四个内角的平分线围成的四边形是__________形.(埴特殊四边形)
参考答案:
【答案】正方
【解析】
此类题根据矩形性质,三角形内角和定理及角平分线定义得到所求的四边形的各个角为90°,进而求解.
∵AF,BE是矩形的内角平分线.
∴∠ABF=∠BAF-90°.
故∠1=∠2=90°.
同理可证四边形GMON四个内角都是90°,则四边形GMON为矩形.
又∵有矩形ABCD且AF、BE、DK、CJ为矩形ABCD四角的平分线,
∴有等腰直角△DOC,等腰直角△AMD,等腰直角△BNC,AD=BC.
∴OD=OC,△AMD≌△BNC,
∴NC=DM,
∴NC-OC=DM-OD,
即OM=ON,
∴矩形GMON为正方形,
故答案为正方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一副直角三角板
 和
和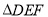 ,
, ,将
,将 和
和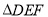 放置如图2的位置,点
放置如图2的位置,点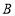 、
、 、
、 、
、 在同一直线上。
在同一直线上。
(1)如图3,
 固定不动,
固定不动,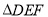 绕点
绕点 逆时针旋转
逆时针旋转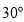 时,判断
时,判断 与
与 的位置关系,并说明理由。
的位置关系,并说明理由。(2)在图2的位置上,
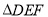 绕点
绕点 逆时针旋转
逆时针旋转 ,在旋转过程中,两个三角形的边是否存在垂直关系?若存在直接写出旋转的角度,并写出哪两边垂直,若不存在,请说明理由。
,在旋转过程中,两个三角形的边是否存在垂直关系?若存在直接写出旋转的角度,并写出哪两边垂直,若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的
 月
月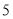 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买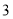 台甲型设备比购买
台甲型设备比购买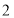 台乙型设备多花
台乙型设备多花 万元,购买
万元,购买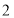 台甲型设备比购买
台甲型设备比购买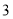 台乙型设备少花
台乙型设备少花 万元.
万元.(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于
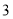 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过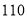 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;(3)在(2)的条件下,已知甲型设备每月的产量为
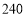 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为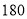 吨.若每月要求产量不低于
吨.若每月要求产量不低于 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数
 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为 ,
, ,
, 的三角形是“和谐三角形”
的三角形是“和谐三角形”概念理解:
如图,
 ,在射线
,在射线 上找一点
上找一点 ,过点
,过点 作
作 交
交 于点
于点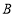 ,以
,以 为端点作射线
为端点作射线 ,交线段
,交线段 于点
于点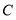 (点
(点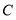 不与
不与 重合)
重合)
(1)
 的度数为 ,
的度数为 , (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”(2)若
 ,求证:
,求证: 是“和谐三角形”.
是“和谐三角形”.应用拓展:
如图,点
 在
在 的边
的边 上,连接
上,连接 ,作
,作 的平分线
的平分线 交于点
交于点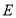 ,在
,在 上取点
上取点 ,使
,使 ,
, .若
.若 是“和谐三角形”,求
是“和谐三角形”,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.

(1)试判断线段BC、DE的数量关系,并说明理由;
(2)若BC平分∠ABD,求证线段FD是线段FG 和 FB的比例中项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点F.

(1)求证:DF⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值.
相关试题

