【题目】如图,已知四边形ABCD是矩形,cot∠ADB=![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.

参考答案:
【答案】(1)20;(2)![]() ,定义域为0<x≤24;(3)20或24或
,定义域为0<x≤24;(3)20或24或![]() .
.
【解析】
试题分析:(1)由矩形的性质和三角函数定义求出AD,由勾股定理求出BD即可;
(2)证明△EDF∽△BDE,得出 ,求出CE=|x﹣12|,由勾股定理求出DE,即可得出结果;
,求出CE=|x﹣12|,由勾股定理求出DE,即可得出结果;
(3)当△DEF是等腰三角形时,△BDE也是等腰三角形,分情况讨论:
①当BE=BD时;②当DE=DB时;③当EB=ED时;分别求出BE即可.
试题解析:(1)∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△BAD中,![]() ,AB=16,
,AB=16,
∴AD=12∴![]() ;
;
(2)∵AD∥BC,
∴∠ADB=∠DBC,
∵∠DEF=∠ADB,
∴∠DEF=∠DBC,
∵∠EDF=∠BDE,
∴△EDF∽△BDE,
∴ ,
,
∵BC=AD=12,BE=x,
∴CE=|x﹣12|,
∵CD=AB=16
∴在Rt△CDE中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,定义域为0<x≤24
,定义域为0<x≤24
(3)∵△EDF∽△BDE,
∴当△DEF是等腰三角形时,△BDE也是等腰三角形,
①当BE=BD时
∵BD=20,∴BE=20
②当DE=DB时,
∵DC⊥BE,∴BC=CE=12,
∴BE=24;
③当EB=ED时,
作EH⊥BD于H,则BH=![]() ,cos∠HBE=cos∠ADB,
,cos∠HBE=cos∠ADB,
即![]()
∴![]() ,
,
解得:BE=![]() ;
;
综上所述,当△DEF时等腰三角形时,线段BE的长为20或24或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角为15°,则这个正多边形的边数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据等式和不等式的性质,可以得到:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系;
(2)已知A=5m2﹣4( m﹣
m﹣  ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某钢厂预计今年的钢产量比去年增加18%,达到260万吨,去年的钢产量是多少?如果设去年的产量为x万吨,则可列方程为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
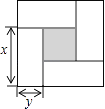
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(5x3+2x4y﹣3xy2)+(x3+3xy2+y3)﹣(6x3﹣x2y2+2y3),其中 x=2,y=﹣1.
相关试题

