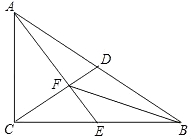
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

参考答案:
【答案】略
【解析】
试题分析:(1)先根据题意得出△ACB∽△ECA,再由直角三角形的性质得出CD=AD,由∠CAD+∠ABC=90°可得出∠ACD+∠EAC=90°,进而可得出∠AFC=90°;
(2)根据AE⊥CD可得出∠EFC=90°,∠ACE=∠EFC,故可得出△ECF∽△EAC,再由点E是BC的中点可知CE=BE,故![]() ,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
试题解析:(1)∵AC2=CECB,
∴![]() .
.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
(2)∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴![]()
∵点E是BC的中点,
∴CE=BE,
∴![]()
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=2x+3中,y随x的增大而_____.(填“增大”或“减小”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角为15°,则这个正多边形的边数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据等式和不等式的性质,可以得到:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系;
(2)已知A=5m2﹣4( m﹣
m﹣  ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,cot∠ADB=
 ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某钢厂预计今年的钢产量比去年增加18%,达到260万吨,去年的钢产量是多少?如果设去年的产量为x万吨,则可列方程为_____.
-
科目: 来源: 题型:
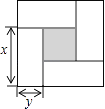
查看答案和解析>>【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49
相关试题

