【题目】如图,直线y=x+b与双曲线y= ![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点. 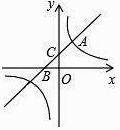
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
参考答案:
【答案】
(1)解:把A(1,2)代入双曲线y= ![]() ,可得k=2,
,可得k=2,
∴双曲线的解析式为y= ![]() ;
;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1
(2)解:设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,
∴B(﹣1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴ ![]() BP×CO=2,即
BP×CO=2,即 ![]() |x﹣(﹣1)|×1=2,
|x﹣(﹣1)|×1=2,
解得x=3或﹣5,
∴P点的坐标为(3,0)或(﹣5,0)
【解析】(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧
 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号) ①若∠PAB=30°,则弧
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号) ①若∠PAB=30°,则弧  的长为π;②若PD∥BC,则AP平分∠CAB;
的长为π;②若PD∥BC,则AP平分∠CAB;
③若PB=BD,则PD=6 ;④无论点P在弧
;④无论点P在弧  上的位置如何变化,CPCQ为定值.
上的位置如何变化,CPCQ为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin60°+|3﹣
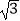 |+(π﹣2)0﹣(
|+(π﹣2)0﹣(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
①已知:如图,在ABCD中,对角线AC,BD交于点O,________.
②求证: -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
课外阅读时间(单位:小时)
频数(人数)
频率
0<t≤2
2
0.04
2<t≤4
3
0.06
4<t≤6
15
0.30
6<t≤8
a
0.50
t>8
5
b

请根据图表信息回答下列问题:
(1)频数分布表中的a= , b=;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.

(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2 .
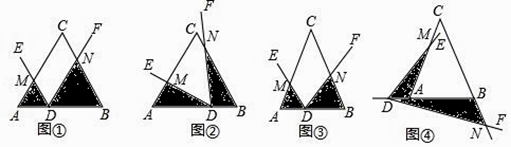
(1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;
(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;
(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
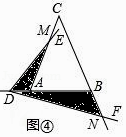
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.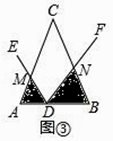
相关试题

